2021-04-20虽然已经拿到了🐧厂的暑期实习offer,但自己基本处于0刷题的状态,想到两个多月之后就要开始秋招(提前批)心里就慌得一匹😟。因此赶紧利用这段时间刷一刷算法题,以免秋招时笔试都过不了🙈。本文主要用来记录刷题过程中自己认为的重点、难点以及自己对各类题型的总结。
1. 数组
1.1 基础知识
- 定义: 数组是存放在
连续内存空间上的相同类型数据的集合。 - 数组的下标都是从0开始。
- 可直接通过下表索引取值。
- 删除或增添元素时,需要移动其他元素的地址。
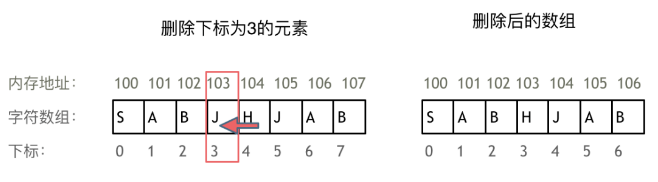
- c++中
vector和array区别:std::vector- 是模板类(template class),是c++特有的结构体。
- 由动态数组实现,不定长,动态管理内存。
- 功能相比
array更多,但效率会低一些。
std::array- 是内置结构体,对标c中的数组。
- 提供连续的、可索引的元素序列。
- 定长,且不能修改(除非是POD平凡数组且由
malloc分配)。
简单总结- 一般情况下无脑用
vector就行。 - 若确定无需改数组大小,用
array速度更快些。
- 一般情况下无脑用
1.2 典型例题
1.2.1 搜索插入位置(No.35)
题目描述
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。你可以假设数组中无重复元素。
示例1:
输入: [1,3,5,6], 5
输出: 2
示例2:
输入: [1,3,5,6], 2
输出: 1
示例3:
输入: [1,3,5,6], 7
输出: 4
示例4:
输入: [1,3,5,6], 0
输出: 0
暴力解法
遍历该有序数组,将每个元素与目标值进行对比,可分为三种情况:
- 当前元素与目标值相等,则直接返回当前元素的索引;
- 当前元素大于目标值,因为是升序,后续元素肯定都大于目标值,则直接返回当前元素索引;
- 当前元素小于目标值,继续循环,若到最后一元素仍小于目标值,则返回当前元素索引+1。
- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.35 搜索插入位置 类型:数组
class Solution35(object):
# 暴力解法
def searchInsert(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
len_array = len(nums)
for i in range(len_array):
if nums[i] >= target: # 大于或等于的情形都是返回i
return i
elif nums[i] < target and i == (len_array -1):
return i + 1
if __name__ == '__main__':
# No.35
s = Solution35()
in_put_1 = [1, 3, 5, 6]
in_put_2 = 5
print(s.searchInsert(in_put_1, in_put_2))二分法
看到题中的数组是有序的应尝试用二分法来解决。二分法的关键是二分后区间的边界定义问题,整体代码要保持始终一致。首先定义两个变量
start和end来确定二分区间[start, end],这里为闭区间,因此循环的终止条件为start > end。对每个二分区间,首先计算其中间元素的全局索引mid = start + (end - start + 1) // 2,然后分三种情况判断:
- 中间元素等于目标值,则直接返回中间元素全局索引;
- 中间元素大于目标值,说明目标值只可能在左二分区间,因此修改右边界
end = mid - 1;- 中间元素小于目标值,说明目标值只可能在右二分区间,因此修改左边界
start = mid + 1- 时间复杂度:
O(logn)- 空间复杂度:
O(1)
# No.35 搜索插入位置 类型:数组
class Solution35(object):
# 二分法
def searchInsertBisection(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
len_array = len(nums)
start = 0
end = len_array - 1
while end >= start: # 二分区间为闭区间[start, end]
mid = start + (end - start + 1) // 2
if nums[mid] == target:
return mid
elif nums[mid] > target:
end = mid - 1
elif nums[mid] < target:
start = mid + 1
return start
if __name__ == '__main__':
# No.35
s = Solution35()
in_put_1 = [1, 3, 5, 6]
in_put_2 = 5
print(s.searchInsertBisection(in_put_1, in_put_2))1.2.2 移除元素(No.27)
题目描述
给你一个数组
nums和一个值val,你需要原地移除所有数值等于val的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用O(1)额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例1:
输入: nums = [3,2,2,3], val = 3
输出: 2, nums = [2,2]
解释: 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例2:
输入: nums = [0,1,2,2,3,0,4,2], val = 2
输出: 5, nums = [0,1,3,0,4]
解释: 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
暴力解法
数组只能覆盖值而不能直接删除,用两层循环即可解决。注意点:
python用for循环在内部改变循环变量仅在该次循环生效,因此这题用while循环更容易写一些。- 第一层循环变量
i以及数组大小size在删除一个元素之后需要-1。- 时间复杂度:
O(n^2)- 空间复杂度:
O(1)
# No.27 移除元素 类型:数组
class Solution27(object):
# 暴力解法
def removeElement(self, nums, val):
"""
:type nums: List[int]
:type val: int
:rtype: int
"""
# for 循环
# num_del = 0
# skip = 0
# for i in range(len(nums)):
# if nums[i - num_del] == val:
# for j in range(len(nums) - (num_del + skip + 1)):
# nums[i - num_del + j] = nums[i - num_del + j + 1]
# num_del += 1
# else:
# skip += 1
#
# return len(nums) - num_del
# while 循环
i = 0
size = len(nums)
while i < size:
if nums[i] == val:
j = i
while j < size - 1:
nums[j] = nums[j + 1]
j += 1
i -= 1
size -= 1
i += 1
return size
if __name__ == '__main__':
# No.27
s = Solution27()
in_put_1 = [3, 2, 2, 3]
in_put_2 = 3
print(s.removeElement(in_put_1, in_put_2))双指针法
通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。双指针法(快慢指针法)在数组和链表的操作中是非常常见的,很多考察数组和链表操作的面试题,都使用双指针法。
核心思路: 上述暴力解法的每次移动元素都是移一步但需移多次,实际上每个不等于var的元素只需移一次,而步长等于该元素前边等于var元素的个数,使用双指针来记录即可:
- 若当前元素不等于
val,则将快指针的值赋予慢指针,然后快慢指针都+1。- 若当前元素等于
val,快指针+1,慢指针不变。- 快指针遍历完整个数组循环结束。
- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.27 移除元素 类型:数组
class Solution27(object):
# --------------------双指针法--------------------
def removeElementDoubleP(self, nums, val):
"""
:type nums: List[int]
:type val: int
:rtype: int
"""
slow_p = 0
for fast_p in range(len(nums)):
if nums[fast_p] != val:
nums[slow_p] = nums[fast_p] # 不等于val的元素只需移动一次,步伐为fast_p - slow_p
slow_p += 1
return slow_p
if __name__ == '__main__':
# No.27
s = Solution27()
in_put_1 = [3, 2, 2, 3]
in_put_2 = 3
print(s.removeElementDoubleP(in_put_1, in_put_2))1.2.3 长度最小的子数组(No.209)
题目描述
给定一个含有
n个正整数的数组和一个正整数target。找出该数组中满足其和≥ target的长度最小的连续子数组[numsl, numsl+1, ..., numsr-1, numsr],并返回其长度。如果不存在符合条件的子数组,返回0。
示例1:
输入: target = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的子数组。
示例2:
输入: target = 4, nums = [1,4,4]
输出: 1
示例3:
输入: target = 11, nums = [1,1,1,1,1,1,1,1]
输出: 0
暴力解法
两层循环,第一层循环遍历整个数组,第二个循环用于对每个元素向后累加,但应该注意,一旦加至满足
>=target的条件,第二层循环就可以跳出。
- 时间复杂度:
O(n^2), 在leetcode上直接超时了😢- 空间复杂度:
O(1)
# No.209 长度最小的子数组 类型:数组
class Solution209(object):
# --------------------暴力解法--------------------
def minSubArrayLen(self, target, nums):
"""
:type target: int
:type nums: List[int]
:rtype: int
"""
min_len = len(nums) + 1
for i in range(len(nums)):
sum_temp = 0
for j in range(len(nums) - i):
sum_temp += nums[i + j]
if sum_temp >= target:
min_len = min(min_len, j + 1)
break # 直接跳出循环
if min_len > len(nums):
return 0
else:
return min_len
if __name__ == '__main__':
# No.209
s = Solution209()
in_put_1 = 7
in_put_2 = [2, 3, 1, 2, 4, 3]
print(s.minSubArrayLen(in_put_1, in_put_2))滑动窗口法
上述暴力解法的缺陷在于第二层循环存在冗余,以
target = 7, nums = [2,3,1,2,4,3]为例,第一次循环得到最小子数组[2,3,1,2],第二次内循环其实没必要计算3+1并判断,因为若3+1>target则第一次循环得到的最小子数组不可能为[2,3,1,2]。滑动窗口法则避免了这种冗余计算,其本质也是一种双指针法,利用两个指针分别指向子序列的头、尾。
- 若子序列之和
<target,则尾指针+1。- 若子序列之和
>target,则记录子序列长度,并将头指针右移,直到子序列之和<target。- 可加一个判断,若子序列长度
=1则直接返回。- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.209 长度最小的子数组 类型:数组
class Solution209(object):
# --------------------滑动窗口法--------------------
def minSubArrayLenSlidingWindow(self, target, nums):
"""
:type target: int
:type nums: List[int]
:rtype: int
"""
start = 0
min_len = len(nums) + 1
sum_temp = 0
for end in range(len(nums)):
sum_temp += nums[end]
while sum_temp >= target:
min_len = min(min_len, end - start + 1)
if min_len == 1: # 大小为1时可直接返回
return min_len
sum_temp -= nums[start]
start += 1
if min_len > len(nums):
return 0
else:
return min_len
if __name__ == '__main__':
# No.209
s = Solution209()
in_put_1 = 7
in_put_2 = [2, 3, 1, 2, 4, 3]
print(s.minSubArrayLenSlidingWindow(in_put_1, in_put_2))1.2.4 螺旋矩阵II(No.59)
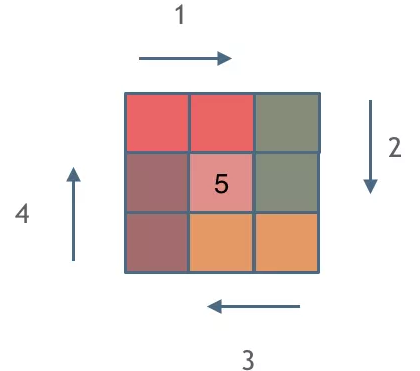
题目描述
给你一个正整数
n,生成一个包含1到n2所有元素,且元素按顺时针顺序螺旋排列的n x n正方形矩阵matrix。
示例1
输入: n = 3
输出: [[1,2,3],[8,9,4],[7,6,5]]
示例2
输入: n = 1
输出: [[1]]
模拟法
模拟矩阵生成的过程,初始位置为左上角,初始方向为右。
- 转变方向判定: 若下一步的位置超出边界或者是之前访问过的位置(被访问过的位置的值都大于0),则顺时针改变一次方向。
- 如此反复填入总共
n^2个元素。- 注意
python列表与常数的乘法:[0] * 3 = [0, 0, 0]- 时间复杂度:
O(n^2)- 空间复杂度:
O(1),不考虑返回的矩阵。
# No.59 螺旋矩阵II 类型:数组
class Solution59(object):
# --------------------模拟法--------------------
def generateMatrix(self, n):
"""
:type n: int
:rtype: List[List[int]]
"""
mat = [[0] * n for _ in range(n)] # 生成全0矩阵
dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)] # 顺时针四个方向
row, col, dirIdx = 0, 0, 0
for i in range(n**2):
mat[row][col] = i + 1
dr, dc = dirs[dirIdx]
r, c = row + dr, col + dc
if r < 0 or r >= n or c < 0 or c >= n or mat[r][c] > 0: # 边界判断,是否换方向
dirIdx = (dirIdx + 1) % 4
dr, dc = dirs[dirIdx]
row, col = row + dr, col + dc
return mat
if __name__ == '__main__':
# No.59
s = Solution59()
in_put = 3
print(s.generateMatrix(in_put))分层模拟法
可以把这种方法比喻为
剥洋葱法,从外至内一层一层计算。定义每一层的左上点、右下点分别为(x1,y1)和(x2,y2),按照顺时针方向计算,每条边的区间为左闭右开。
- 每记算完一层,就将左上点与右下点
内缩。- 循环终止条件为左上点与右下点错位。
- 若
n为奇数,则手动补最中心点的值。- 时间复杂度:
O(n^2)- 空间复杂度:
O(1), 不考虑返回的矩阵。
# No.59 螺旋矩阵II 类型:数组
class Solution59(object):
# --------------------分层模拟法--------------------
def generateMatrixLayer(self, n):
"""
:type n: int
:rtype: List[List[int]]
"""
mat = [[0] * n for _ in range(n)] # 生成全0矩阵
x1, y1, x2, y2 = 0, 0, n - 1, n - 1 # 左上、右下点
num = 1
while x1 <= x2 and y1 <= y2:
for i in range(y2 - y1): # 向右
mat[x1][y1 + i] = num
num += 1
for i in range(x2 - x1): # 向下
mat[x1 + i][y2] = num
num += 1
for i in range(y2 - y1): # 向左
mat[x2][y2 - i] = num
num += 1
for i in range(x2 - x1): # 向上
mat[x2 - i][y1] = num
num += 1
x1 += 1
y1 += 1
x2 -= 1
y2 -= 1
if n % 2: # n为奇数时处理中心点
mat[n // 2][n // 2] = n ** 2
return mat
if __name__ == '__main__':
# No.59
s = Solution59()
in_put = 3
print(s.generateMatrixLayer(in_put))1.2.5 顺时针打印矩阵(No.JZ29)
class SolutionJZ29(object):
def spiralOrder(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
if not matrix:
return []
# 方向模拟
# dirs = [(0,1),(1,0),(0,-1),(-1,0)]
# m = len(matrix)
# n = len(matrix[0])
# idx,x,y = 0,0,-1
# s = set()
# res = []
# for i in range(m*n):
# d = dirs[idx]
# nx,ny = x+d[0], y+d[1]
# if nx<0 or ny<0 or nx>=m or ny>=n or (nx,ny) in s:
# idx = (idx + 1) % 4
# d = dirs[idx]
# nx,ny = x+d[0], y+d[1]
# res.append(matrix[nx][ny])
# s.add((nx,ny))
# x,y = nx,ny
# return res
# 边界模拟
l,t,r,b = 0,0,len(matrix[0])-1,len(matrix)-1
res = []
while True:
for i in range(l,r+1): res.append(matrix[t][i])
t += 1
if t > b: break
for i in range(t,b+1): res.append(matrix[i][r])
r -= 1
if l > r: break
for i in range(r,l-1,-1): res.append(matrix[b][i])
b -= 1
if t > b: break
for i in range(b,t-1,-1): res.append(matrix[i][l])
l += 1
if l > r: break
return res1.2.6 二维数组中的查找(No.JZ4)
class SolutionJZ4(object):
def findNumberIn2DArray(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if not matrix or not matrix[0]:
return False
# 二分法
# m,n = len(matrix), len(matrix[0])
# for i in range(m):
# row = matrix[i]
# if target < row[0]:
# return False
# elif target > row[-1]:
# continue
# l, r = 0, n - 1
# while l <= r:
# mid = (l+r) // 2
# if row[mid] == target:
# return True
# elif row[mid] > target:
# r = mid - 1
# else:
# l = mid + 1
# return False
# 线性查找
i, j = len(matrix) - 1, 0
while i >= 0 and j < len(matrix[0]):
if matrix[i][j] == target:
return True
elif matrix[i][j] > target:
i -= 1
else:
j += 1
return False1.2.7 接雨水(No.42)
class Solution42(object):
def trap(self, height):
"""
:type height: List[int]
:rtype: int
"""
# 暴力法,超时
# res = 0
# for i in range(len(height)):
# m_l,m_r = 0,0
# for j in range(i,len(height)):
# m_r = max(m_r, height[j])
# for j in range(i,-1,-1):
# m_l = max(m_l, height[j])
# res += min(m_l,m_r) - height[i]
# return res
# 额外数组记录左右最大值
# m_l = [0] * len(height)
# temp_l = height[0]
# for i in range(len(height)):
# m_l[i] = max(temp_l,height[i])
# temp_l = m_l[i]
# m_r = [0] * len(height)
# temp_r = height[-1]
# for i in range(len(height)-1,-1,-1):
# m_r[i] = max(temp_r,height[i])
# temp_r = m_r[i]
# res = 0
# for i in range(len(height)):
# res += min(m_l[i],m_r[i]) - height[i]
# return res
# 双指针
res = 0
l,r = 0,len(height) - 1
m_l,m_r = 0,0
while l < r:
if height[l] < height[r]:
m_l = max(m_l,height[l])
res += m_l - height[l]
l += 1
else:
m_r = max(m_r, height[r])
res += m_r - height[r]
r -= 1
return res1.2.8 扑克牌中的顺子(No.JZ61)
class SolutionJZ61(object):
def isStraight(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
# 计算0的数量,遍历抵消
nums = sorted(nums)
num_0 = 0
for i in nums:
if i == 0: num_0 += 1
else: break
# for i in range(num_0+1, len(nums)):
# if nums[i] == nums[i - 1] + 1:
# continue
# elif nums[i] == nums[i - 1]:
# return False
# else:
# num_0 -= (nums[i] - nums[i -1] - 1)
# if num_0 < 0:
# return False
# return True
# max-min<5
min_num = nums[num_0]
max_num = nums[-1]
if max_num - min_num >= 5:
return False
for i in range(num_0+1, len(nums)):
if nums[i] == nums[i-1]:
return False
return True1.2.9 和为s的两个数字(No.JZ57)
class SolutionJZ57(object):
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
l, r = 0, len(nums)-1
while l < r:
if nums[l] + nums[r] > target:
r -= 1
elif nums[l] + nums[r] < target:
l += 1
else:
return [nums[l],nums[r]]1.2.10 和为s的连续正数序列(No.JZ57II)
class SolutionJZ57II:
def findContinuousSequence(self, target: int) -> List[List[int]]:
# 数学计算,确定序列的长度上限,对固定的长度可解得序列起始点
n = int((math.sqrt(1+8*target)-1) / 2)
res = []
for i in range(n, 1, -1):
if int((2*target/i + 1 - i) / 2) != (2*target/i + 1 - i) / 2:
continue
else:
idx = int((2*target/i + 1 - i) / 2)
res.append([j for j in range(idx, idx + i)])
return res
# 滑动窗口
# i, j = 1,2
# res = []
# while i < j:
# if (i+j)*(j-i+1)/2 == target:
# res.append([k for k in range(i,j+1)])
# j += 1
# elif (i+j)*(j-i+1)/2 > target:
# i += 1
# else:
# j += 1
# return res1.2.11 调整数组顺序使奇数位于偶数前面(No.JZ21)
class SolutionJZ21:
def exchange(self, nums: List[int]) -> List[int]:
# 双指针
l,r = 0,len(nums)-1
while l<r:
while l<r and nums[r]%2==0: r-=1
while l<r and nums[l]%2==1: l+=1
nums[l],nums[r] = nums[r],nums[l]
return nums1.2.12 合并两个有序数组(No.88)
class Solution88:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
# 正序双指针,额外数组
# res = [0] * (m+n)
# i,j,k = 0,0,0
# while i<m or j<n:
# if j>=n or i<m and nums1[i]<=nums2[j]:
# res[k] = nums1[i]
# i += 1
# elif i>=m or j<n and nums1[i]>nums2[j]:
# res[k] = nums2[j]
# j += 1
# k += 1
# for i in range(m+n):
# nums1[i] = res[i]
# 逆序双指针
p1,p2,k = m-1,n-1,m+n-1
while k >= 0:
if p2<0 or p1>=0 and nums1[p1]>=nums2[p2]:
nums1[k] = nums1[p1]
p1 -= 1
# elif p1<0 or p2>=0 and nums1[p1]<nums2[p2]:
else:
nums1[k] = nums2[p2]
p2 -= 1
k -= 11.2.13 寻找旋转排序数组中的最小值(No.153)
class Solution153:
def findMin(self, nums: List[int]) -> int:
# 二分法,每次需和右边界比较,不能与左边界比较
left,right = 0,len(nums)-1
while left < right:
mid = (left+right) // 2
if nums[mid] > nums[right]: # 最小值在右区间
left = mid + 1
elif nums[mid] < nums[right]: # 最小值在左区间
right = mid
return nums[left]1.2.14 寻找旋转排序数组中的最小值II(No.154)
class Solution154:
def findMin(self, nums: List[int]) -> int:
# 二分法,考虑重复情况
left, right = 0, len(nums) - 1
while left < right:
mid = (left + right) // 2
if nums[mid] > nums[right]: # 最小值在右区间
left = mid + 1
elif nums[mid] < nums[right]: # 最小值在左区间
right = mid
else:
right -= 1 # 相等无法判断,右边界减一缩小区间
return nums[left]1.2.15 搜索旋转排序数组(No.33)
class Solution33:
def search(self, nums: List[int], target: int) -> int:
# 二分法
left,right = 0,len(nums)-1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
if nums[mid] > nums[right]: # mid 在左区间
if target >= nums[left] and target < nums[mid]: # target在[l,mid)
right = mid - 1
else:
left = mid + 1
else: # mid 在右区间
if target > nums[mid] and target <= nums[right]: # target在(mid,right]
left = mid + 1
else:
right = mid - 1
return -11.2.16 搜索旋转排序数组II(No.81)
class Solution81:
def search(self, nums: List[int], target: int) -> bool:
# 二分法
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return True
if nums[mid] > nums[right]: # mid在左区间
if target >= nums[left] and target < nums[mid]:
right = mid - 1
else:
left = mid + 1
elif nums[mid] < nums[right]: # mid在右区间
if target > nums[mid] and target <= nums[right]:
left = mid + 1
else:
right = mid - 1
else:
right -= 1
return False1.2.17 下一个排列(No.31)
class Solution31:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
# 从后向前找到第一个相邻升序对(i,j),此时[j,end]一定降序
# 从后遍历[j,end],找到第一个大于nums[i]的数nums[k],交换nums[i],nums[k]
# 将[j,end]升序
n = len(nums)
flag = False
for i in range(n-1,0,-1):
if nums[i] > nums[i-1]:
flag = True
for k in range(n-1,i-1,-1):
if nums[k] > nums[i-1]:
nums[i-1],nums[k] = nums[k],nums[i-1]
break
break
if not flag: i = 0
for j in range((n-i)//2):
nums[j+i],nums[n-1-j] = nums[n-1-j],nums[j+i]1.2.18 合并区间(No.56)
class Solution56:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
length = len(intervals)
if length == 1:
return intervals
# 按区间左边界排序
intervals = sorted(intervals, key = lambda x:x[0])
res = []
left = intervals[0]
# 逐个遍历合并
for i in range(length-1):
right = intervals[i+1]
if right[0] <= left[1]:
left = [left[0],max(left[1],right[1])]
else:
res.append(left)
left = right
res.append(left)
return res1.2.19 删除有序数组中的重复项(No.26)
class Solution26:
def removeDuplicates(self, nums: List[int]) -> int:
length = len(nums)
if length <= 1:
return length
# 解决这类问题的通用思路:
# idx指向要填的位置,可初始化为可以重复的值k,i遍历整个数组
# 若nums[i]与idx前k个数都相同,则继续,否则在idx处填入nums[i],idx++
idx = 1
for i in range(1,length):
if nums[i] == nums[idx-1]:
continue
else:
nums[idx] = nums[i]
idx += 1
return idx1.2.20 删除有序数组中的重复项II(No.80)
class Solution80:
def removeDuplicates(self, nums: List[int]) -> int:
length = len(nums)
if length <= 2:
return length
idx = 2
for i in range(2,length):
if nums[i]==nums[idx-1] and nums[i]==nums[idx-2]:
continue
else:
nums[idx] = nums[i]
idx += 1
return idx1.3 典型例题
1.3.1 寻找两个正序数组的中位数(No.4)
class Solution4:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
# 合并两个正序数组,O(m+n)
# def merge_two(nums1,nums2):
# m,n = len(nums1),len(nums2)
# if m==0: return nums2
# if n==0: return nums1
# ans = [0] * (m+n)
# i,j,k = 0,0,0
# while i<m or j<n:
# if j==n:
# ans[k] = nums1[i]
# i += 1
# elif i==m:
# ans[k] = nums2[j]
# j += 1
# elif nums1[i] <= nums2[j]:
# ans[k] = nums1[i]
# i += 1
# elif nums1[i] > nums2[j]:
# ans[k] = nums2[j]
# j += 1
# k += 1
# return ans
# merged_nums = merge_two(nums1,nums2)
# length = len(merged_nums)
# return merged_nums[length//2] if length%2==1 else (merged_nums[length//2]+merged_nums[length//2-1])/2
# 二分法,中位数的性质:两边元素个数相同,左边最大值小于右边最小值
# nums1为长度较小的数组
if len(nums1) > len(nums2):
nums1, nums2 = nums2, nums1
m,n = len(nums1), len(nums2)
# 分割线左边元素总数
cnt_left = (m+n+1) // 2
# 在 nums1 的区间 [0, m] 里查找恰当的分割线,
# 使得 nums1[i - 1] <= nums2[j] && nums2[j - 1] <= nums1[i]
left, right = 0,m
while left < right:
i = left + (right-left+1)//2 # 向上取整
j = cnt_left - i
if nums1[i-1] > nums2[j]:
right = i-1
else:
left = i
i = left
j = cnt_left - i
# 处理特殊情况
nums1LeftMax = float('-inf') if i == 0 else nums1[i-1]
nums1RightMin = float('inf') if i == m else nums1[i]
nums2LeftMax = float('-inf') if j == 0 else nums2[j-1]
nums2RightMin = float('inf') if j == n else nums2[j]
if (m+n) % 2==1:
return max(nums1LeftMax, nums2LeftMax)
else:
return (max(nums1LeftMax, nums2LeftMax) + min(nums1RightMin, nums2RightMin)) / 21.3.2 缺失的第一个正数(No.41)
class Solution41:
def firstMissingPositive(self, nums: List[int]) -> int:
# 原地哈希,未出现的最小正数取值范围为[1,n+1]
# 交换,使得下标i对应i+1
n = len(nums)
for i in range(n):
while 1<=nums[i]<=n and nums[i]!=i+1 and nums[nums[i]-1]!=nums[i]:
nums[nums[i]-1],nums[i] = nums[i],nums[nums[i]-1]
# 遍历查找
for i in range(1,n+1):
if i != nums[i-1]:
return i
return n+11.3.3 数组中重复的数据(No.442)
class Solution442:
def findDuplicates(self, nums: List[int]) -> List[int]:
# 原地哈希
n = len(nums)
for i in range(n):
while nums[nums[i]-1] != nums[i]:
nums[nums[i]-1], nums[i] = nums[i], nums[nums[i]-1]
res = []
for i in range(n):
if nums[i] != i+1:
res.append(nums[i])
return res1.3.4 找到所有数组中消失的数字(No.448)
class Solution448:
def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
# 原地哈希
n = len(nums)
for i in range(n):
while nums[nums[i]-1] != nums[i]:
nums[nums[i]-1], nums[i] = nums[i], nums[nums[i]-1]
res = []
for i in range(n):
if i+1 != nums[i]:
res.append(i+1)
return res1.3.5 旋转图像(No.48)
class Solution48:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
# 思路:沿对角线翻转一次,再水平翻转一次
n = len(matrix)
# 对角线翻转
for i in range(n):
for j in range(i+1,n):
matrix[i][j],matrix[j][i] = matrix[j][i],matrix[i][j]
# 水平翻转
for i in range(n):
for j in range(n//2):
matrix[i][j],matrix[i][n-j-1] = matrix[i][n-j-1],matrix[i][j]1.3.6 在排序数组中查找元素的第一个和最后一个位置(No.34)
class Solution34:
def searchRange(self, nums: List[int], target: int) -> List[int]:
# 两次二分法
if not nums:
return [-1,-1]
left,right = 0,len(nums)-1
# 找最左边的target
while left<right:
mid = left + (right-left)//2
if nums[mid] == target:
right = mid
elif nums[mid] > target:
right = mid - 1
else:
left = mid + 1
if nums[left] != target:
return [-1,-1]
l,r = left,len(nums)-1
# 找最右边的target
while l<r:
mid = l + (r-l+1)//2 # 注意需要向上取整
if nums[mid] == target:
l = mid
elif nums[mid] < target:
l = mid + 1
else:
r = mid-1
return [left,l]1.3.7 搜索二维矩阵II(No.240)
class Solution240:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
# 从右上角开始搜索,一步步缩行缩列
m,n = len(matrix),len(matrix[0])
i,j = 0,n-1
while i<m and j>=0:
if matrix[i][j] == target:
return True
elif matrix[i][j] > target:
j -= 1
else:
i += 1
return False1.3.8 寻找峰值(No.162)
class Solution162:
def findPeakElement(self, nums: List[int]) -> int:
# 二分法,往递增的方向缩进
left,right = 0,len(nums)-1
while left<right:
mid = left + (right-left)//2
if mid > 0 and nums[mid-1]<nums[mid] and nums[mid+1]<nums[mid]:
return mid
if nums[mid] < nums[mid+1]:
left = mid + 1
else:
right = mid
return left1.3.9 在D天内送达包裹的能力(No.1011)
class Solution1011:
def shipWithinDays(self, weights: List[int], days: int) -> int:
# 二分法,对最低运载能力二分
def check(mid):
need_days = 0
sum_weight = 0
for i in range(len(weights)):
sum_weight += weights[i]
if sum_weight > mid:
need_days += 1
sum_weight = weights[i]
return need_days+1 > days
left, right = max(weights), sum(weights)
while left < right:
mid = left + (right - left) // 2
if check(mid):
left = mid + 1
else:
right = mid
return left1.3.10 跳跃游戏(No.55)
class Solution55:
def canJump(self, nums: List[int]) -> bool:
# 贪心,遍历更新最远距离
max_dis = 0
for i,num in enumerate(nums):
if i > max_dis:
return False
max_dis = max(max_dis, i + nums[i])
if max_dis >= len(nums) - 1:
return True1.3.11 跳跃游戏II(No.45)
class Solution:
def jump(self, nums: List[int]) -> int:
# [start,end)为遍历的范围
start = 0
end = 1
res = 0
while end < len(nums):
max_dis = 0
for i in range(start,end):
max_dis = max(max_dis, i + nums[i])
start = end
end = max_dis + 1
res += 1
return res1.4 数组总结
- 数组最重要的特性: 内存空间是
连续的。 - 删除或增添元素时,需移动其他元素。
有序数组应尝试二分法。- 双指针法在数组与链表中很常见。
- 滑动窗口法是一种较为巧妙的双指针法。
区间定义很重要,确定之后整个程序应保持一致。- 涉及需内部改循环变量的情况,
python中用while循环更好。 - 模拟类题需重视
边界条件。
2. 链表
2.1 基础知识
- 定义: 链表是一种通过指针串联在一起的线性结构,每一个节点是由两部分组成,一个是
数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(即空指针)。 - 单链表
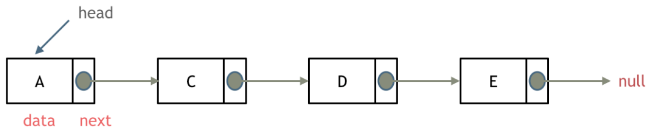
- 双链表
- 每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。
- 既可以向前查询也可以向后查询。
- 循环链表
- 链表首尾相连。
- 可以用来解决约瑟夫环问题。
- 存储方式: 链表中的节点在内存中不是连续分布的,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理。
- 链表节点定义
struct ListNode {
int val; // 节点上存储的元素
ListNode *next; // 指向下一个节点的指针
ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
};class ListNode(object):
def __init__(self, val=0, next=None):
self.val = val
self.next = next
# 双链表
class ListNodeDouble(object):
def __init__(self, val=0, next=None, prev=None):
self.val = val
self.next = next
self.prev = prev- 删除节点: 将指向要删除节点的指针指向下一个节点。
- 添加节点: 将插入处前节点指向插入节点,再将插入节点指向插入处后节点。
- 性能对比:
数组: 插入or删除O(n)| 查询O(1)| 适用于数据量固定、频繁查询、较少增删的场景链表: 插入or删除O(1)| 查询O(n)| 适用于数据量不固定、频繁增删、较少查询的场景
2.2 典型例题
2.2.1 移除链表元素(No.203)
题目描述
给你一个链表的头节点
head和一个整数val,请你删除链表中所有满足Node.val == val的节点,并返回新的头节点。
示例1
输入: head = [1,2,6,3,4,5,6], val = 6
输出: [1,2,3,4,5]
示例2
输入: head = [ ], val = 1
输出: [ ]
示例3
输入: head = [7,7,7,7], val = 7
输出: [ ]
一般方法
- 一般节点的处理方式很简单,即将指向要删除节点的指针指向下一个节点。
- 头结点分开处理,若头结点的值等于目标值,则直接将头指针向后移一位。
- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.203 移除链表元素 类型:链表
class Solution203(object):
# --------------------一般方法--------------------
def removeElements(self, head, val):
"""
:type head: ListNode
:type val: int
:rtype: ListNode
"""
# 处理头节点
while head and head.val == val:
head = head.next
cur = head
while cur and cur.next: # 需要cur不为None,否则cur.next会报错,输入为[]的情形
if cur.next.val == val:
cur.next = cur.next.next
else:
cur = cur.next
return head
if __name__ == '__main__':
# --------------------打印链表--------------------
def print_list(head):
while head:
print(head.val)
head = head.next
# No.203
s = Solution203()
in_put_4 = ListNode(val=2, next=None)
in_put_3 = ListNode(val=4, next=in_put_4)
in_put_2 = ListNode(val=3, next=in_put_3)
head = ListNode(val=7, next=in_put_2)
val = 4
result = s.removeElements(head, val)
print_list(result)哨兵节点法(伪头)
哨兵节点广泛应用于树和链表中,如伪头、伪尾、标记等,它们是纯功能的,通常不保存任何数据,其主要目的是使链表标准化,如使链表永不为空、永不无头、简化插入和删除。
- 这题哨兵节点将被用于
伪头。- 由于加了
伪头,原来的头结点可以当做普通节点处理。- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.203 移除链表元素 类型:链表
class Solution203(object):
# --------------------哨兵节点法--------------------
def removeElementsSentinel(self, head, val):
"""
:type head: ListNode
:type val: int
:rtype: ListNode
"""
sentinel = ListNode(0, head)
cur = sentinel
while cur.next: # 不需要cur判断,因为cur取不到None
if cur.next.val == val:
cur.next = cur.next.next
else:
cur = cur.next
return sentinel.next
if __name__ == '__main__':
# No.203
s = Solution203()
in_put_4 = ListNode(val=2, next=None)
in_put_3 = ListNode(val=4, next=in_put_4)
in_put_2 = ListNode(val=3, next=in_put_3)
head = ListNode(val=7, next=in_put_2)
val = 4
result = s.removeElementsSentinel(head, val)
print_result(result)2.2.2 设计链表(No.707)
题目描述
设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:
val和next,val是当前节点的值,next是指向下一个节点的指针/引用。如果要使用双向链表,则还需要一个属性prev以指示链表中的上一个节点。假设链表中的所有节点都是0-index的。
在链表类中实现这些功能:
get(index): 获取链表中第 index 个节点的值。如果索引无效,则返回-1。addAtHead(val): 在链表的第一个元素之前添加一个值为 val 的节点。插入后,新节点将成为链表的第一个节点。addAtTail(val): 将值为 val 的节点追加到链表的最后一个元素。addAtIndex(index,val): 在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度,则该节点将附加到链表的末尾。如果 index 大于链表长度,则不会插入节点。如果index小于0,则在头部插入节点。deleteAtIndex(index): 如果索引 index 有效,则删除链表中的第 index 个节点。
示例1MyLinkedList linkedList = new MyLinkedList(); linkedList.addAtHead(1); linkedList.addAtTail(3); linkedList.addAtIndex(1,2); //链表变为1-> 2-> 3 linkedList.get(1); //返回2 linkedList.deleteAtIndex(1); //现在链表是1-> 3 linkedList.get(1); //返回3
单链表
哨兵节点用作伪头在链表操作中十分有用,初始化一个链表需指定
size和head(伪头)属性。
- 单链表的节点应具备两个属性:
val和next。- 增加或删除元素后应记得对
size进行同步加减。- 时间复杂度:
addAtHead:O(1)addAtTail:O(n),n为链表长度。addAtIndex,get,deleteAtIndex:O(k),k为索引。
# No.707 设计链表 类型:链表
# --------------------单链表法--------------------
class MyLinkedList(object):
def __init__(self):
self.size = 0
self.head = ListNode(0) # 哨兵节点,用作伪头
def get(self, index):
"""
:type index: int
:rtype: int
"""
if (self.size < index + 1) or index < 0: # 索引无效,返回-1
return -1
cur = self.head
for i in range(index + 1):
cur = cur.next
return cur.val
def addAtHead(self, val):
"""
:type val: int
:rtype: None
"""
old_head = self.head.next # 原来的头结点
added_head = ListNode(val)
self.head.next = added_head # 将哨兵节点指向新头
added_head.next = old_head # 将新头指向旧头
self.size += 1 # 链表长度加1
def addAtTail(self, val):
"""
:type val: int
:rtype: None
"""
tail = ListNode(val)
cur = self.head
# while cur.next: # 若当前节点指向不为空,则当前节点后移一位,直到最后一个节点
for i in range(self.size): # 利用size信息可以指定移动次数
cur = cur.next
cur.next = tail # 将最后的节点指向tail
self.size += 1 # 链表长度加1
def addAtIndex(self, index, val):
"""
:type index: int
:type val: int
:rtype: None
"""
if index <= 0: # 插入头节点
self.addAtHead(val)
elif 0 < index < self.size: # 插入中间节点
left = self.head
insert = ListNode(val)
for i in range(index): # 从伪头移动到插入处左节点
left = left.next
right = left.next # 插入处右节点
left.next = insert # 令左节点指向插入节点
insert.next = right # 插入节点指向右节点
self.size += 1 # 链表长度加1
elif index == self.size: # 插入尾节点
self.addAtTail(val)
def deleteAtIndex(self, index):
"""
:type index: int
:rtype: None
"""
if (self.size >= index + 1) and index >= 0: # 索引有效
left = self.head
for i in range(index): # 从伪头移动到删除处左节点
left = left.next
right = left.next.next # 删除处右节点
left.next = right # 左节点直接指向右节点
self.size -= 1 # 链表长度减1
if __name__ == '__main__':
# No.707
s = MyLinkedList()
s.addAtHead(1)
s.addAtTail(3)
s.addAtIndex(1, 2)
print(s.get(1))
s.deleteAtIndex(1)
print(s.get(1))双链表法
双链表与单链表最大的不同之处在于每个节点不仅保存指向下一个节点的指针,也保存了指向前一个节点的指针,因此查询时可以双向。
- 双链表具备的属性:
val,next,prev。- 效率比单链表高,但占的空间多一些。
- 初始化时不仅需要
伪头,也需要伪尾。- 时间复杂度:
addAtHead,addAtTail:O(1)get,addAtIndex,deleteAtIndex:O(min(k, n-k)),k为索引,n为链表长度。- 空间复杂度:
O(1)
# No.707 设计链表 类型:链表
# --------------------双链表法--------------------
class MyLinkedListDouble(object):
def __init__(self):
self.size = 0
self.head, self.tail = ListNodeDouble(0), ListNodeDouble(0) # 哨兵节点,用作伪头、伪尾
self.head.next = self.tail
self.tail.prev = self.head
def get(self, index):
"""
:type index: int
:rtype: int
"""
if (self.size < index + 1) or index < 0: # 索引无效,返回-1
return -1
if (index + 1) <= self.size // 2:
cur = self.head
for _ in range(index + 1): # 依次向后查询
cur = cur.next
else:
cur = self.tail
for i in range(self.size - index): # 依次向前查询
cur = cur.prev
return cur.val
def addAtHead(self, val):
"""
:type val: int
:rtype: None
"""
self.addAtIndex(0, val)
def addAtTail(self, val):
"""
:type val: int
:rtype: None
"""
self.addAtIndex(self.size, val)
def addAtIndex(self, index, val):
"""
:type index: int
:type val: int
:rtype: None
"""
if index > self.size:
return
if index < 0:
index = 0
insert = ListNodeDouble(val)
if (index + 1) <= self.size // 2:
cur = self.head
for _ in range(index): # 依次向后查询
cur = cur.next
# 插入新节点
insert.next = cur.next
cur.next.prev = insert
insert.prev = cur
cur.next = insert
else:
cur = self.tail
for i in range(self.size - index): # 依次向前查询
cur = cur.prev
# 插入新节点
cur.prev.next = insert
insert.prev = cur.prev
insert.next = cur
cur.prev = insert
self.size += 1 # 链表长度加1
def deleteAtIndex(self, index):
"""
:type index: int
:rtype: None
"""
if (self.size >= index + 1) and index >= 0: # 索引有效
if (index + 1) <= self.size // 2:
cur = self.head
for _ in range(index): # 依次向后查询
cur = cur.next
# 删除节点
cur.next = cur.next.next
cur.next.prev = cur
else:
cur = self.tail
for i in range(self.size - index - 1): # 依次向前查询, 注意这里的循环范围与添加节点不一样!!!
cur = cur.prev
# 删除节点
cur.prev = cur.prev.prev
cur.prev.next = cur
self.size -= 1 # 链表长度减1
if __name__ == '__main__':
# No.707
s_d = MyLinkedListDouble()
s_d.addAtHead(1)
s_d.addAtTail(3)
s_d.addAtIndex(1, 2)
print(s_d.get(1))
s_d.deleteAtIndex(1)
print(s_d.get(1))2.2.3 反转链表(No.206)
题目描述
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
双指针法(迭代)
并不需要定义一个新的链表,可以在原链表上直接修改元素指针的方向。
- 定义
pre指针,记录前元素,需初始化为None。- 定义
cur指针,记录当前元素,循环终止条件为cur is None。- 定义
temp指针,记录后元素,因为修改cur指针后无法通过cur来获取后续节点信息。- 直接用
head替代cur也行,减少占用空间。- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.206 反转链表 类型:链表
class Solution206(object):
# --------------------双指针法-------------------
def reverseList(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
pre = None # 需初始化为None
cur = head
while cur:
temp = cur.next # 在将当前节点指向前节点之前,需要储存下一节点
cur.next = pre # 将当前节点反转
# 后移一位
pre = cur
cur = temp
return pre
if __name__ == '__main__':
# No.206
s = Solution206()
in_put = MyLinkedList()
for i in range(5):
in_put.addAtTail(i + 1)
print_list(in_put.head.next)
result = s.reverseList(in_put.head.next)
print_list(result)递归法
递归法更为抽象一些,最重要的是反向过程的设计。
- 递归的跳出条件要确定,即当前元素或下一元素为空。
- 关键语句
head.next.next = head,用来反转,即将当前元素的下一元素指向当前元素。- 一次反转后,链表变为
1->2->3->4和None<-4<-5。- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.206 反转链表 类型:链表
class Solution206(object):
# --------------------递归法-------------------
def reverseListRecursion(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if head is None or head.next is None: # 递归跳出条件
return head
new_head = self.reverseListRecursion(head.next)
head.next.next = head # 反转
head.next = None # 保证反转后链表末尾为None
return new_head
if __name__ == '__main__':
# No.206
s = Solution206()
in_put = MyLinkedList()
for i in range(5):
in_put.addAtTail(i + 1)
print_list(in_put.head.next)
result_R = s.reverseListRecursion(in_put.head.next)
print_list(result_R)2.2.4 删除链表的倒数第N个节点(No.19)
题目描述
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例1
输入: head = [1,2,3,4,5], n = 2
输出: [1,2,3,5]
示例2
输入: head = [1], n = 1
输出: []
示例3
输入: head = [1,2], n = 1
输出: [1]
一般方法
最容易想到的方法是先遍历一遍链表获得链表长度,然后就能确定需删除元素的索引,再遍历至对应位置进行删除操作即可。
- 添加哨兵节点,可以将头节点一般化。
- 时间复杂度:
O(L),L为链表长度。- 空间复杂度:
O(1)
# No.19 删除链表的倒数第N个节点 类型:链表
class Solution19(object):
# --------------------一般方法-------------------
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
# 获取链表长度
cur = head
size = 0
while cur:
size += 1
cur = cur.next
n = size - n # 顺序索引, n取值范围为[0, size-1]
# 删除索引为n的节点
sentinel = ListNode(0) # 伪头
sentinel.next = head
left = sentinel
for i in range(n): # 后移至索引节点前一个
left = left.next
left.next = left.next.next # 删除节点
return sentinel.next
if __name__ == '__main__':
# No.19
s = Solution19()
in_put = MyLinkedList()
for i in range(5):
in_put.addAtTail(i + 1)
print_list(in_put.head.next)
result = s.removeNthFromEnd(in_put.head.next, 2)
print_list(result)双指针法
相比于一般方法,双指针法只需遍历一遍。
- 初始化快指针指向
head,慢指针指向伪头。- 核心思想是假设快指针指向的节点就是要删除的节点,那么快指针往后移动
n-1步就到链表末尾了。- 若快指针移动
n-1步没到末尾,则快慢指针同步移动,直至末尾,此时慢指针指向的就是待删除节点的前一节点。- 时间复杂度:
O(L),L为链表长度。- 空间复杂度:
O(1)
# No.19 删除链表的倒数第N个节点 类型:链表
class Solution19(object):
# --------------------双指针法-------------------
def removeNthFromEndDouble(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
sentinel = ListNode(0) # 伪头
sentinel.next = head
slow = sentinel
fast = head
count = 0 # 让快指针先走n-1步,之后再同步走
while fast.next:
fast = fast.next
count += 1
if count > n - 1:
slow = slow.next
slow.next = slow.next.next # 删除节点
return sentinel.next
if __name__ == '__main__':
# No.19
s = Solution19()
in_put = MyLinkedList()
for i in range(5):
in_put.addAtTail(i + 1)
print_list(in_put.head.next)
result_D = s.removeNthFromEndDouble(in_put.head.next, 2)
print_list(result_D)2.2.5 环形链表II(No.142)
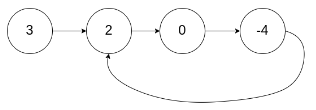
题目描述
给定一个链表,返回链表开始入环的第一个节点。如果链表无环,则返回
null。为了表示给定链表中的环,我们使用整数pos来表示链表尾连接到链表中的位置(索引从0开始)。如果pos是-1,则在该链表中没有环。注意,pos仅仅是用于标识环的情况,并不会作为参数传递到函数中。不允许修改给定的链表。
示例
输入: head = [3,2,0,-4], pos = 1
输出: 返回索引为 1 的链表节点
解释: 链表中有一个环,其尾部连接到第二个节点。
双指针法
可以将该题分为两个部分,第一部分为判断是否有环,第二部分为确定入环节点。
- 定义快慢两个指针,慢指针每次移一步,快指针每次移两步。
- 如果有环,则快指针一定能追上慢指针。
- 确定入环节点比较巧妙,需要一定的数学计算。相遇时,慢指针走了
a+b,快指针走了a+b+n(b+c),由于快指针速度是慢指针两倍,则有等式2(a+b)=a+b+n(b+c),解得a=c+(n-1)(b+c)- 即从相遇点到入环点的距离加上
n-1环长等于从链表头到入环点的距离。因此令快指针重新指向head,然后和慢指针同步向后每次移一位,它们最终在入环节点处相遇。- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.142 环形链表II 类型:链表
class Solution142(object):
# --------------------双指针法-------------------
def detectCycle(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
# 初始化快慢指针
fast = head
slow = head
while fast:
# 无环则直接返回
if fast.next is None or fast.next.next is None:
return
slow = slow.next # 慢指针移一步
fast = fast.next.next # 快指针移两步
if fast == slow: # 若快指针追上慢指针,则一定有环
fast = head # 将快指针指向head
# 快慢指针同步移动,相遇处即入环节点
while fast != slow:
fast = fast.next
slow = slow.next
return slow
if __name__ == '__main__':
# No.142
s = Solution142()
node_1 = ListNode(3)
node_2 = ListNode(2)
node_3 = ListNode(0)
node_4 = ListNode(-4)
node_1.next = node_2
node_2.next = node_3
node_3.next = node_4
node_4.next = node_2
result = s.detectCycle(node_1)
print(result.val)2.2.6 链表中倒数第k个节点(No.JZ22)
class SolutionJZ22(object):
def getKthFromEnd(self, head, k):
"""
:type head: ListNode
:type k: int
:rtype: ListNode
"""
l = 0
cur = head
while cur:
l += 1
cur = cur.next
k = l - k + 1
res = head
for i in range(k-1):
res = res.next
return res2.2.7 从尾到头打印链表(No.JZ6)
class SolutionJZ6(object):
def reversePrint(self, head):
"""
:type head: ListNode
:rtype: List[int]
"""
# 辅助栈
# temp = []
# while head:
# temp.append(head.val)
# head = head.next
# res = []
# while temp:
# res.append(temp.pop())
# return res
# 递归
def recur(head):
if not head:
return []
return recur(head.next) + [head.val]
return recur(head)2.2.8 两数相加(No.2)
class Solution2(object):
def addTwoNumbers(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
res = ListNode(0)
cur = res
temp = 0
while True:
cur.val = (l1.val + l2.val + temp) % 10
temp = (l1.val + l2.val + temp) // 10
if not l1.next and not l2.next:
break
if not l1.next:
l1.next = ListNode(0)
if not l2.next:
l2.next = ListNode(0)
cur.next = ListNode(0)
cur = cur.next
l1 = l1.next
l2 = l2.next
# 最后还有进位的话需要补一位
if temp:
cur.next = ListNode(temp)
return res2.2.9 合并两个排序的链表(No.JZ25)
class SolutionJZ25(object):
def mergeTwoLists(self, l1, l2):
"""
:type l1: ListNode
:type l2: ListNode
:rtype: ListNode
"""
# 哨兵节点
# sen = ListNode(0)
# cur = sen
# while l1 and l2:
# if l1.val <= l2.val:
# cur.next = l1
# l1 = l1.next
# else:
# cur.next = l2
# l2 = l2.next
# cur = cur.next
# cur.next = l1 if l1 else l2
# return sen.next
# 递归
if not l1: return l2
if not l2: return l1
if l1.val <= l2.val:
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
else:
l2.next = self.mergeTwoLists(l1, l2.next)
return l22.2.10 K 个一组翻转链表(No.25)
class Solution25:
def reverseKGroup(self, head: ListNode, k: int) -> ListNode:
def reverse(head):
pre = None
cur = head
while cur:
post = cur.next
cur.next = pre
pre = cur
cur = post
return pre
# 哨兵节点,拆开--》翻转--》连接
sen = ListNode(0)
sen.next = head
pre,end = sen,sen
while end.next:
for i in range(k):
if end:
end = end.next
else: break
if not end: break
post = end.next
start = pre.next
end.next = None
pre.next = reverse(start)
start.next = post
pre = start
end = pre
return sen.next2.2.11 两个链表的第一个公共节点(No.JZ52)
class SolutionJZ52:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
# 暴力法超时O(N^2)
# a,b = headA,headB
# while a:
# while b:
# if a == b:
# return a
# b = b.next
# a = a.next
# b = headB
# return
# 哈希表
# dic = set()
# a,b = headA,headB
# while a:
# if not a in dic:
# dic.add(a)
# a = a.next
# while b:
# if b in dic:
# return b
# b = b.next
# return
# 双指针循环遍历,走的路为重复长度加各自独立长度
if not headA or not headB:
return
a,b = headA,headB
while a or b:
if a == b:
return a
a = headB if not a else a.next
b = headA if not b else b.next
return2.2.12 LRU 缓存机制(No.146)
class Node:
def __init__(self,key=0,val=0,pre=None,nex=None):
self.key = key
self.val = val
self.pre = pre
self.next = nex
class DoubleList:
def __init__(self,size=0):
self.size = size
# 伪头,伪尾
self.head = Node()
self.tail = Node()
self.head.next, self.tail.pre = self.tail, self.head
# 加入头结点
def addfirst(self,node):
temp = self.head.next
self.head.next = node
node.pre = self.head
node.next = temp
temp.pre = node
self.size += 1
# 删除某个节点
def remove(self,node):
pre,nex = node.pre,node.next
pre.next,nex.pre = nex,pre
self.size -= 1
# 删除尾部节点,并返回该节点
def removelast(self):
node = self.tail.pre
node.pre.next,self.tail.pre = self.tail,node.pre
self.size -= 1
return node
class LRUCache:
def __init__(self, capacity: int):
self.capacity = capacity
self.dic = dict()
self.cache = DoubleList()
def get(self, key: int) -> int:
if key not in self.dic:
return -1
else:
node = self.dic[key]
self.cache.remove(node)
self.cache.addfirst(node)
return node.val
def put(self, key: int, value: int) -> None:
if key in self.dic:
node = self.dic[key]
node.val = value
self.cache.remove(node)
self.cache.addfirst(node)
else:
if self.cache.size >= self.capacity:
last_node = self.cache.removelast()
self.dic.pop(last_node.key)
node = Node(key,value)
self.cache.addfirst(node)
self.dic[key] = node2.2.13 反转链表II(No.92)
class Solution92:
def reverseBetween(self, head: ListNode, left: int, right: int) -> ListNode:
# 头插法, start为开始翻转的前一个节点
sen = ListNode(0)
sen.next = head
start,cur = sen,head
for i in range(left - 1):
start = cur
cur = cur.next
temp = cur
# 不断地将cur后面的节点删除并加入到start后边
for i in range(right - left):
nex = cur.next
cur.next = cur.next.next # 删除节点
start.next = nex
nex.next = temp
temp = nex
return sen.next2.2.14 合并K个升序链表(No.23)
class Solution23:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
# 两两合并
def mergetwo(l1,l2):
if not l1: return l2
if not l2: return l1
if l1.val <= l2.val:
l1.next = mergetwo(l1.next, l2)
return l1
else:
l2.next = mergetwo(l1,l2.next)
return l2
if not lists: return
n = len(lists)
l1 = lists[0]
for i in range(1,n):
l2 = lists[i]
l1 = mergetwo(l1,l2)
return l12.2.15 重排链表(No.143)
class Solution143:
def reorderList(self, head: ListNode) -> None:
"""
Do not return anything, modify head in-place instead.
"""
def my_reverse(l):
pre = None
cur = l
while cur:
temp = cur.next
cur.next = pre
pre = cur
cur = temp
return pre
length,cur = 0,head
while cur:
cur = cur.next
length += 1
if length <= 2:
return head
# 找到分割节点
n1 = length // 2
cur = head
for i in range(n1):
cur = cur.next
# 把链表分为两部分l1,l2,并将l2翻转
l2 = cur.next
l2 = my_reverse(l2)
cur.next = None
l1 = head
while l2:
temp1 = l1.next
l1.next = l2
temp2 = l2.next
l2.next = temp1
l1 = temp1
l2 = temp2
return head2.3 典型例题
2.3.1 排序链表(No.148)
class Solution148:
def sortList(self, head: ListNode) -> ListNode:
# 暴力法
# vals = []
# cur = head
# while cur:
# vals.append(cur.val)
# cur = cur.next
# vals = sorted(vals)
# cur = head
# i = 0
# while cur:
# cur.val = vals[i]
# i += 1
# cur = cur.next
# return head
# 归并排序(递归)
def recur(head):
if not head or not head.next:
return head
# 快慢指针找到链表中点
slow, fast = head, head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
right_head = slow.next
slow.next = None # 截断
left = recur(head)
right = recur(right_head)
# merge
cur = sen = ListNode(0) # 辅助节点
while left and right:
if left.val <= right.val:
cur.next = left
left = left.next
else:
cur.next = right
right = right.next
cur = cur.next
cur.next = left if left else right
return sen.next
return recur(head)2.3.2 回文链表(No.234)
class Solution:
def isPalindrome(self, head: ListNode) -> bool:
# O(n)时间复杂度 O(1)空间复杂度 翻转链表
# 找到中间节点
def my_reverse(head):
pre = None
cur = head
while cur:
temp = cur.next
cur.next = pre
pre = cur
cur = temp
return pre
slow,fast = head,head
while fast.next and fast.next.next:
slow = slow.next
fast = fast.next.next
# 翻转后半部分链表
post = my_reverse(slow.next)
p1,p2 = head,post
while p2:
if p1.val != p2.val:
return False
p1 = p1.next
p2 = p2.next
return True2.4 链表总结
- 类型: 单链表、双链表、循环链表。
- 存储方式: 离散,通过指针连在一起。
- 性能: 查询慢,插入/删除快。
- 涉及头节点需要额外处理的,使用哨兵节点当做伪头十分有效。
- 反转链表经常考察,要掌握迭代和递归法。
- 循环链表应考虑双指针法。
3. 哈希表
3.1 基础知识
- 定义: 哈希表(Hash table)是根据
关键码的值而直接进行访问的数据结构。 - 数组就是一张哈希表。
- 哈希表一般都是用于快速判断一个元素是否出现在集合里。
- 哈希函数: 通过
hashcode将其他数据格式转化为不同的数值,再进行取模,就能得到哈希表的索引。 - 哈希碰撞: 若输入大小大于哈希表的大小,则会出现多对一的现象,即多个输入对应哈希表的同一个位置。一般解决方法有二:
- 拉链法: 将发生冲突的元素存储在链表中。
- 线性探测法: 该方法要求
tablesize大于datasize,依靠哈希表中的空位来解决碰撞问题。
- 常见的三种哈希结构:
数组、set(集合)、map(映射)
3.2 典型例题
3.2.1 有效的字母异位词(No.242)
题目描述
给定两个字符串
s和t,编写一个函数来判断t是否是s的字母异位词。你可以假设字符串只包含小写字母。
示例1
输入: s = “anagram”, t = “nagaram”
输出: true
示例2
输入: s = “rat”, t = “car”
输出: false
排序法
两个字符串互为异位词等价于
两个字符串排序后相等。
- 若字符串长度不等,直接返回
False- 分别对字符串
s和t进行排序。- 排序后相等则返回
True否则返回False。- 时间复杂度:
O(nlogn),排序为O(nlogn),比较是否相等为O(n)- 空间复杂度:
O(logn)
# No.242 有效的字母异位词 类型:哈希表
class Solution242(object):
# --------------------排序法--------------------
def isAnagram(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
# 若字符串长度不等,则直接返回False
if len(s) != len(t):
return False
# 排序
s = sorted(s)
t = sorted(t)
return s == t
if __name__ == '__main__':
# No.242
s = Solution242()
in_put1 = 'anagram'
in_put2 = 'nagaram'
result = s.isAnagram(in_put1, in_put2)
print(result)哈希表
若只考虑26个小写字母,则可以创建一个数组来记录每个字符出现的频次。若考虑
unicode字符,则使用哈希表(python中用dict即可)。
- 若字符串长度不等,直接返回
False。- 遍历第一个字符串,记录字符频次。
- 遍历第二个字符串,减去对应的频次。若数组元素出现负数,则返回
False。python中获取单个字符编码:ord()- 时间复杂度:
O(n)- 空间复杂度:
O(S),S=26为字符集大小。- 若利用
python内置模块,则一句代码搞定:return collections.Counter(s) == collections.Counter(t),需import collections。
# No.242 有效的字母异位词 类型:哈希表
class Solution242(object):
# --------------------哈希表(数组)--------------------
def isAnagramArray(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
# 若字符串长度不等,则直接返回False
if len(s) != len(t):
return False
temp = [0] * 26 # 初始化大小为26的table
for i in s:
temp[ord(i) - ord('a')] += 1
for j in t:
temp[ord(j) - ord('a')] -= 1
if temp[ord(j) - ord('a')] < 0:
return False
return True
# --------------------哈希表(字典)--------------------
def isAnagramArrayDict(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
# 若字符串长度不等,则直接返回False
if len(s) != len(t):
return False
temp = {}
for i in s:
if i not in temp:
temp[i] = 0
temp[i] += 1
for j in t:
if j not in temp:
return False
temp[j] -= 1
if temp[j] < 0:
return False
return True
if __name__ == '__main__':
# No.242
s = Solution242()
in_put1 = 'an#gram'
in_put2 = 'nagaram'
result_A = s.isAnagramArray(in_put1, in_put2)
result_D = s.isAnagramArrayDict(in_put1, in_put2)
print(result_A)
print(result_D)3.2.2 两个数组的交集(No.349)
题目描述
给定两个数组,编写一个函数来计算它们的交集。
示例1
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2]
示例2
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [9,4]
暴力解法
遍历数组1,对其每个元素判断是否在数组2中。
- 时间复杂度:
O(mn),m、n分别为数组1、数组2大小。- 空间复杂度:
O(1)
# No.349 两个数组的交集 类型:哈希表
class Solution349(object):
# --------------------暴力解法--------------------
def intersection(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: List[int]
"""
result = []
# 遍历数组1
for i in nums1:
if i in nums2 and i not in result: # 若i在数组2中且不在result列表中,则将其加入至result
result.append(i)
return result
if __name__ == '__main__':
# No.349
s = Solution349()
in_put1 = [1, 2, 2, 1]
in_put2 = [2, 2]
result = s.intersection(in_put1, in_put2)
print(result)哈希表
如果使用哈希集合存储元素,则可以在
O(1)的时间内判断一个元素是否在集合中,从而降低时间复杂度。
python中使用set()即可构建哈希集合。- 对较短的哈希集合进行遍历,判断其元素是否在较长的哈希集合中。
- 时间复杂度:
O(m+n)- 空间复杂度:
O(m+n)- 空间换时间。
# No.349 两个数组的交集 类型:哈希表
class Solution349(object):
# --------------------哈希表法--------------------
def intersectionHash(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: List[int]
"""
# 转化为哈希集合
set1 = set(nums1)
set2 = set(nums2)
# 遍历较短的哈希集合
if len(set1) < len(set2):
return [x for x in set1 if x in set2]
else:
return [x for x in set2 if x in set1]
if __name__ == '__main__':
# No.349
s = Solution349()
in_put1 = [1, 2, 2, 1]
in_put2 = [2, 2]
result_H = s.intersectionHash(in_put1, in_put2)
print(result_H)3.2.3 快乐数(No.202)
题目描述
编写一个算法来判断一个数
n是不是快乐数。「快乐数」定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为
1,也可能是无限循环但始终变不到1。- 如果可以变为
1,那么这个数就是快乐数。
示例1
输入: 19
输出: true
解释:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
示例2
输入: n = 2
输出: false
哈希集合
该问题可分为两个部分,第一部分为获取下一个数,第二部分为判断是否循环。
- 取数的各个位思路: 将数对
10取余即得最后一位,再将数对10整除,循环直至n//10 = 0。也可考虑将数转为字符串遍历。- 判断是否循环思路: 涉及多次判断一个数是否在集合里,应使用哈希表。
- 时间复杂度:
O(logn),获取下一个数的时间占主导。- 空间复杂度:
O(logn)
# No.202 快乐数 类型:哈希表
class Solution202(object):
# --------------------哈希表(哈希集合)法--------------------
def isHappy(self, n):
"""
:type n: int
:rtype: bool
"""
log = {n} # 初始化哈希集合
while n != 1:
temp = str(n)
new_n = 0
for i in temp: # 获取下一个数
new_n += int(i)**2
# 判断是否循环
if new_n in log:
return False
log.add(new_n)
n = new_n
return True
if __name__ == '__main__':
# No.202
s = Solution202()
in_put = 19
result = s.isHappy(in_put)
print(result)双指针法
反复获取下一个数其实构成了一个隐式的链表,因此问题就转化为链表是否有环,用快慢指针法即可解决。
- 慢指针每次走一步,快指针每次走两步。
- 若快指针追上慢指针,则有环。
- 否则快指针将先到
1。- 时间复杂度:
O(logn)- 空间复杂度:
O(1)
# No.202 快乐数 类型:哈希表
class Solution202(object):
# --------------------双指针法--------------------
def isHappyDouble(self, n):
"""
:type n: int
:rtype: bool
"""
def get_next(n):
sum = 0
while n > 0:
n, digit = divmod(n, 10)
sum += digit**2
return sum
fast = n
slow = n
while fast != 1:
slow = get_next(slow) # 慢指针走一步
fast = get_next(get_next(fast)) # 快指针走两步
if fast == 1:
return True
if slow == fast: # 快指针追上慢指针,说明有环
return False
return True
if __name__ == '__main__':
# No.202
s = Solution202()
in_put = 19
result_D = s.isHappyDouble(in_put)
print(result_D)3.2.4 两数之和(No.1)
题目描述
给定一个整数数组
nums和一个整数目标值target,请你在该数组中找出和为目标值的那两个整数,并返回它们的数组下标。
示例1
输入: nums = [2,7,11,15], target = 9
输出: [0,1]
示例2
输入: nums = [3,2,4], target = 6
输出: [1,2]
示例3
输入: nums = [3,3], target = 6
输出: [0,1]
暴力解法
两层循环遍历即可。
- 时间复杂度:
O(n^2)- 空间复杂度:
O(1)
# No.1 两数之和 类型:哈希表
class Solution1(object):
# --------------------暴力解法--------------------
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
# 两层循环遍历
for i in range(len(nums)):
for j in range(len(nums)-i-1):
if nums[i] + nums[j+1+i] == target:
return [i, j+1+i]
return []
if __name__ == '__main__':
# No.1
s = Solution1()
in_put_1 = [2, 7, 11, 15]
in_put_2 = 9
result = s.twoSum(in_put_1, in_put_2)
print(result)哈希表
使用哈希表可以降低查找的时间复杂度,考虑到需要返回下标,所以使用
dict数据结构。c++中则使用map。
- 注意要避免元素与自身匹配,因此将元素加入哈希表的操作应在查找之后。
- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.1 两数之和 类型:哈希表
class Solution1(object):
# --------------------哈希表(字典)--------------------
def twoSumHash(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
hash_t = {}
for i, num in enumerate(nums):
if target - num in hash_t: # 哈希表查找
return [i, hash_t[target - num]]
hash_t[num] = i # 需在查找操作之后
return []
if __name__ == '__main__':
# No.1
s = Solution1()
in_put_1 = [2, 7, 11, 15]
in_put_2 = 9
result_H = s.twoSumHash(in_put_1, in_put_2)
print(result_H)3.2.5 四数相加II(No.454)
题目描述
给定四个相同长度的包含整数的数组列表
A,B,C,D,计算有多少个元组(i, j, k, l),使得A[i] + B[j] + C[k] + D[l] =0
示例
输入:
A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]
输出: 2
两个元组为(0, 0, 0, 1), (1, 1, 0, 0)
暴力解法
使用4层循环遍历。
leetcode上直接超出时间限制。
- 时间复杂度:
O(n^4)- 空间复杂度:
O(1)
# No.454 四数相加II 类型:哈希表
class Solution454(object):
# --------------------暴力解法--------------------
def fourSumCount(self, nums1, nums2, nums3, nums4):
"""
:type nums1: List[int]
:type nums2: List[int]
:type nums3: List[int]
:type nums4: List[int]
:rtype: int
"""
# 四层循环
count = 0
for i in nums1:
for j in nums2:
for k in nums3:
for l in nums4:
if nums1[i]+nums2[j]+nums3[k]+nums4[l] == 0:
count += 1
return count
if __name__ == '__main__':
# No.454
s = Solution454()
in_put_1 = [1, 2]
in_put_2 = [-2, -1]
in_put_3 = [-1, 2]
in_put_4 = [0, 2]
result = s.fourSumCount(in_put_1, in_put_2, in_put_3, in_put_4)
print(result)哈希表
将四个数组分为两组,A、B一组,C、D一组。
- 遍历A、B,将A、B之和哈希表存储。可用
python自带模块一行完成:sum_12 = collections.Counter(num1+num2 for num1 in nums1 for num2 in nums2)- 遍历C、D,若负CD之和在哈希表中,则次数增加对应的值。
- 时间复杂度:
O(n^2)- 空间复杂度:
O(n^2)
# No.454 四数相加II 类型:哈希表
class Solution454(object):
# --------------------哈希表法(字典)--------------------
def fourSumCountHash(self, nums1, nums2, nums3, nums4):
"""
:type nums1: List[int]
:type nums2: List[int]
:type nums3: List[int]
:type nums4: List[int]
:rtype: int
"""
count = 0
sum_12 = {}
# 将AB之和用哈希表存储,键为和,值为出现的次数
for num1 in nums1:
for num2 in nums2:
if num1 + num2 not in sum_12:
sum_12[num1 + num2] = 0
sum_12[num1 + num2] += 1
# 对CD之和进行遍历,若负CD之和在哈希表中,则次数增加对应的值
for num3 in nums3:
for num4 in nums4:
if -(num3 + num4) in sum_12:
count += sum_12[-(num3 + num4)]
return count
if __name__ == '__main__':
# No.454
s = Solution454()
in_put_1 = [1, 2]
in_put_2 = [-2, -1]
in_put_3 = [-1, 2]
in_put_4 = [0, 2]
result_H = s.fourSumCountHash(in_put_1, in_put_2, in_put_3, in_put_4)
print(result_H)
Update(2021.06.24)一看两个多月没刷题了,赶紧利用实习摸鱼的时间热热手😏
3.2.6 赎金信(No.383)
题目描述
给定一个赎金信
ransom字符串和一个杂志magazine字符串,判断第一个字符串ransom能不能由第二个字符串magazines里面的字符构成。如果可以构成,返回true;否则返回false。为了不暴露赎金信字迹,要从杂志上搜索各个需要的字母,组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。
示例
ransomNote = “aa”, magazine = “aab”
输出: true
直接法
- 直接在
python自带字符串数据结构上进行操作。- 遍历
ransom字符串,对每一字符,判断其在不在magazine字符串中。- 若在,则删除
magazine中对应的字符并继续循环,若不在则直接返回False。- 时间复杂度:
O(n^2)- 空间复杂度:
O(1)
# No.383 赎金信 类型:哈希表
class Solution383(object):
# --------------------直接法--------------------
def canConstruct(self, ransomNote, magazine):
"""
:type ransomNote: str
:type magazine: str
:rtype: bool
"""
for i in ransomNote: # 遍历赎金信
if i in magazine:
magazine = magazine.replace(i, '', 1) # 若杂志中含有该字母,则将该字母从杂志中移除,并继续循环
continue
else:
return False
return True
if __name__ == "__main__":
s = Solution383()
result = s.canConstruct('haha', 'jacshnkah')
print(result)哈希表(字典)
- 用字典来存储
magazine中每个字符出现的次数。- 遍历
ransom字符串,对每一字符,判断其在不在magazine字典中。- 若在,则对应值减一,不在则直接返回
False。- 利用
collections模块可一行解决:return True if len(collections.Counter(ransomNote) - collections.Counter(magazine))==0 else False- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.383 赎金信 类型:哈希表
class Solution383(object):
# --------------------哈希表(字典)--------------------
def canConstructDict(self, ransomNote, magazine):
# 构建哈希表,值为字符出现的次数
hash_mag = {}
for i in magazine:
if i not in hash_mag:
hash_mag[i] = 0
hash_mag[i] += 1
# 遍历赎金信
for j in ransomNote:
if j in hash_mag:
hash_mag[j] -= 1
if hash_mag[j] < 0:
return False
else:
return False
return True
if __name__ == "__main__":
s = Solution383()
result_D = s.canConstructDict('haha', 'jacshnkah')
print(result)3.2.7 三数之和(No.15)
题目描述
给你一个包含
n个整数的数组nums,判断nums中是否存在三个元素a,b,c,使得a + b + c = 0 ?请你找出所有和为0且不重复的三元组。答案中不可以包含重复的三元组。
示例
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
哈希表
- 该题使用哈希表十分复杂,主要是因为需要进行去重。
- 下面的代码去重部分时间复杂度太高。
LeetCode上运行直接超时。
# No.15 三数之和 类型:哈希表
class Solution15(object):
# --------------------哈希表--------------------
def threeSumHash(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
result = []
result_hash = []
hash_set = {}
# 哈希表key为bc之和,value为对应的索引
for i in range(len(nums)):
for j in range(len(nums) - 1 - i):
bc = nums[i] + nums[i + j + 1]
if not bc in hash_set:
hash_set[bc] = []
hash_set[bc].append([i, i + j + 1])
# 遍历a
for i in range(len(nums)):
a = nums[i]
if -a in hash_set:
for bc in hash_set[-a]:
if i in [bc[0], bc[1]]:
continue
if {a, nums[bc[0]], nums[bc[1]]} in result_hash: # 去重很关键
continue
result_hash.append({a, nums[bc[0]], nums[bc[1]]})
result.append([a, nums[bc[0]], nums[bc[1]]])
return result
if __name__ == "__main__":
# No.15 三数之和
s = Solution15()
result = s.threeSumHash([-1,0,1,2,-1,-4])
print(result)双指针法
- 双指针法较为简单。首先对数组进行排序,若数组首位大于零,则直接返回
[]。- 初始时
a下标为i,遍历整个数组,b(左指针)下标为i+1,c(右指针)取数组最后一个。- 计算三数之和,若大于零,则右指针向左移一位;若小于零,左指针向右移一位;若相等则记录结果。
- 注意去重,例子
[0,0,0,0]可作为特殊情况进行检验。- 时间复杂度:
O(n^2)- 空间复杂度:
O(logn)
# No.15 三数之和 类型:哈希表
class Solution15(object):
# --------------------双指针法--------------------
def threeSumDoubleP(self, nums):
result = []
nums = sorted(nums)
if nums[0] > 0:
return []
for i in range(len(nums)-2):
if i > 0 and nums[i] == nums[i-1]: # a去重
continue
idx_a = i
idx_b = i + 1 # 左指针
idx_c = len(nums) - 1 # 右指针
while idx_b != idx_c: # 左右指针相遇时跳出
three_sum = nums[idx_a] + nums[idx_b] + nums[idx_c]
if three_sum > 0:
idx_c -= 1
elif three_sum < 0:
idx_b += 1
else:
result.append([nums[idx_a], nums[idx_b], nums[idx_c]])
idx_c -= 1
while nums[idx_c] == nums[idx_c + 1] and idx_b != idx_c: # c去重
idx_c -= 1
return result
if __name__ == "__main__":
# No.15 三数之和
s = Solution15()
in_put = [-1,0,1,2,-1,-4]
result_d = s.threeSumDoubleP(in_put)
print(result_d)3.2.8 四数之和(No.18)
题目描述
给定一个包含
n个整数的数组nums和一个目标值target,判断nums中是否存在四个元素a,b,c和d,使得a + b + c + d的值与target相等?找出所有满足条件且不重复的四元组。答案中不可以包含重复的四元组。
示例
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
双指针法
- 做过三数之和之后再做这道题就容易多了,还是用双指针法更为简单。
- 问题可以转化为遍历第一个数,再在剩余数组做三数之和,同样注意去重。
- 时间复杂度:
O(n^3)- 空间复杂度:
O(logn)
# No.18 四数之和 类型:哈希表
class Solution18(object):
# --------------------双指针法--------------------
def fourSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[List[int]]
"""
nums = sorted(nums)
result = []
for i in range(len(nums) - 3):
if i > 0 and nums[i] == nums[i - 1]: # a去重
continue
for j in range(len(nums) - i - 3):
if j > 0 and nums[i + j + 1] == nums[i + j]: # b去重
continue
idx_a = i
idx_b = i + j + 1
idx_c = idx_b + 1 # 左指针
idx_d = len(nums) - 1 # 右指针
while idx_c < idx_d: # 左右指针相遇时跳出
four_sum = nums[idx_a] + nums[idx_b] + nums[idx_c] + nums[idx_d]
if four_sum > target:
idx_d -= 1
elif four_sum < target:
idx_c += 1
else:
result.append([nums[idx_a], nums[idx_b], nums[idx_c], nums[idx_d]])
idx_d -= 1
while nums[idx_d] == nums[idx_d + 1] and idx_c < idx_d: # d去重
idx_d -= 1
return result
if __name__ == "__main__":
# No.18 四数之和
s = Solution18()
in_put = [1, 0, -1, 0, -2, 2]
# in_put = [2, 2, 2, 2, 2]
target = 0
# target = 8
result = s.fourSum(in_put, target)
print(result)3.2.9 数组中重复的数字(No.M3)
class SolutionM3(object):
def findRepeatNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# h_t = set()
# for i in nums:
# if i not in h_t:
# h_t.add(i)
# else:
# return i
# 利用数组下标信息原地交换,0(1)空间复杂度,原地哈希
length = len(nums)
i = 0
while i < length:
if nums[i] == i:
i += 1
continue
if nums[nums[i]] == nums[i]:
return nums[i]
nums[nums[i]], nums[i] = nums[i], nums[nums[i]]
return -13.2.10 第一个只出现一次的字符(No.JZ50)
class SolutionJZ50:
def firstUniqChar(self, s: str) -> str:
res = ' '
if not s:
return res
d = dict()
for c in s:
if not c in d:
d[c] = 0
d[c] += 1
for i in d:
if d[i] == 1:
return i
return res3.2.11 数组中出现次数超过一半的数字(No.JZ39)
class SolutionJZ39:
def majorityElement(self, nums: List[int]) -> int:
# 哈希表
# n = len(nums)
# d = dict()
# for i in nums:
# if not i in d:
# d[i] = 0
# d[i] += 1
# if d[i] > n//2:
# return i
# 摩尔投票法,对拼消耗
votes = 0
for i in nums:
if votes == 0:
x = i
if x != i:
votes -= 1
else:
votes += 1
return x3.2.12 复杂链表的复制(No.JZ35)
"""
# Definition for a Node.
class Node:
def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
self.val = int(x)
self.next = next
self.random = random
"""
class SolutionJZ35:
def copyRandomList(self, head: 'Node') -> 'Node':
# return copy.deepcopy(head)
# 哈希表
if not head: return
dic,cur = {},head
while cur:
dic[cur] = Node(cur.val)
cur = cur.next
cur = head
while cur:
if cur.next:
dic[cur].next = dic[cur.next]
else:
dic[cur].next = None
if cur.random:
dic[cur].random = dic[cur.random]
else:
dic[cur].random = None
cur = cur.next
return dic[head]3.2.13 最长连续序列(No.128)
class Solution128:
def longestConsecutive(self, nums: List[int]) -> int:
# 哈希表,对起始点分析
nums = set(nums)
res = 0
for i in nums:
if not i-1 in nums: # 只有某个数能作为序列起始点才进入循环
cur_length = 1
while i + 1 in nums:
cur_length += 1
i += 1
res = max(res, cur_length)
return res3.3 哈希表总结
- 当需要快速判断一个元素是否出现在集合里时,需要优先考虑哈希表。
- 哈希函数是把传入的key映射到符号表的索引上。
- 哈希碰撞处理有多个key映射到相同索引上时的情景,处理碰撞的普遍方式是拉链法和线性探测法。
- 在
python中,dict类型就是由哈希表实现的。但要注意仅对字典的key进行哈希操作,因此i in dict的时间复杂度为O(1),但i in dict.values()的时间复杂度为O(N)。 - 在例如三数之和、四数之和等需要去重的题目时,用哈希表比较麻烦,需要考虑双指针法。
4. 字符串
4.1 典型例题
4.1.1 反转字符串(No.344)
题目描述
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组
char[]的形式给出。不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用O(1)的额外空间解决这一问题。你可以假设数组中的所有字符都是ASCII码表中的可打印字符。
示例
输入:[“h”,”e”,”l”,”l”,”o”]
输出:[“o”,”l”,”l”,”e”,”h”]
题解
- 遍历字符串(只需遍历一半),与对应字符交换位置。
- 交换时额外申明一个
temp变量,不用额外创建数组。- 时间复杂度:
O(n)- 空间复杂度:
O(1)
# No.344 反转字符串 类型:字符串
class Solution344(object):
def reverseString(self, s):
"""
:type s: List[str]
:rtype: None Do not return anything, modify s in-place instead.
"""
length = len(s)
for i in range(length // 2):
# 交换字符
temp = s[i]
s[i] = s[length - 1 - i]
s[length - 1 - i] = temp
return s
if __name__ == "__main__":
# No.344 反转字符串
s = Solution344()
in_put = ["h","e","l","l","o"]
result = s.reverseString(in_put)
print(result)4.1.2 反转字符串II(No.541)
题目描述
给定一个字符串
s和一个整数k,你需要对从字符串开头算起的每隔2k个字符的前k个字符进行反转。如果剩余字符少于k个,则将剩余字符全部反转。如果剩余字符小于2k但大于或等于k个,则反转前k个字符,其余字符保持原样。
示例
输入: s = “abcdefg”, k = 2
“bacdfeg”
题解
for循环的写法是关键,每隔2k进行一次反转即可。- 可以用自带的反转函数
reversed()。str.join()用str来连接列表中的字符。- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.541 反转字符串II 类型:字符串
class Solution541(object):
def reverseStr(self, s, k):
"""
:type s: str
:type k: int
:rtype: str
"""
a = list(s)
for i in range(0, len(a), 2 * k):
a[i:i+k] = reversed(a[i:i+k])
return ''.join(a)
if __name__ == "__main__":
# No.541 反转字符串II
s = Solution541()
in_put1 = "abcdefghijklmn"
in_put2 = 2
result = s.reverseStr(in_put1, in_put2)
print(result)4.1.3 替换空格(No.J5)
题目描述
请实现一个函数,把字符串
s中的每个空格替换成”%20”。
示例
输入:s = “We are happy.”
输出:”We%20are%20happy.”
题解
- 对
python来说字符串的处理比较方便,一层for循环遍历即可。- 使用自带的
replace方法可以一行解决。- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.J5 替换空格 类型:字符串
class SolutionJ5(object):
def replaceSpace(self, s):
"""
:type s: str
:rtype: str
"""
a = list(s)
for i, char in enumerate(a):
if char == ' ':
a[i] = '%20'
return ''.join(a)
# OneLine
# return s.replace(' ', '%20')
if __name__ == "__main__":
# No.J5 替换空格
s = SolutionJ5()
in_put = 'We are happy.'
result = s.replaceSpace(in_put)
print(result)4.1.4 翻转字符串里的单词(No.151)
题目描述
给你一个字符串
s,逐个翻转字符串中的所有单词。单词是由非空格字符组成的字符串,s中使用至少一个空格将字符串中的单词分隔开。请你返回一个翻转s中单词顺序并用单个空格相连的字符串。输入字符串s可以在前面、后面或者单词间包含多余的空格。翻转后单词间应当仅用一个空格分隔。翻转后的字符串中不应包含额外的空格。
示例
输入:s = “ Bob Loves Alice “
输出:”Alice Loves Bob”
题解
- 遍历字符串,关键在于确定单词的起点和终点,这里设置
pre指针来辅助判断。- 使用自带函数
split()、reversed()能够一行解决。- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.151 翻转字符串里的单词 类型:字符串
class Solution151(object):
def reverseWords(self, s):
"""
:type s: str
:rtype: str
"""
s = s + ' ' # 处理最后一位无空格情况
ret = ''
start = 0
pre = 0
for i, char in enumerate(s):
if s[pre] == ' ' and s[i] != ' ':
start = i
elif s[pre] != ' ' and s[i] == ' ':
end = i
ret = s[start:end] + ' ' + ret
pre = i
return ret.strip() # 去除末尾空格
# OneLine
# return ' '.join(reversed(s.split()))
if __name__ == "__main__":
# No.151 翻转字符串里的单词
s = Solution151()
in_put = " Bob Loves Alice "
result = s.reverseWords(in_put)
print(result)4.1.5 左旋转字符串(No.J58II)
题目描述
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串”abcdefg”和数字2,该函数将返回左旋转两位得到的结果”cdefgab”。
示例
输入: s = “abcdefg”, k = 2
输出: “cdefgab”
题解
- 字符串切片再相加,
python一行解决- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.J58II 左旋转字符串 类型:字符串
class SolutionJ58II(object):
def reverseLeftWords(self, s, n):
"""
:type s: str
:type n: int
:rtype: str
"""
return s[n:] + s[:n]
if __name__ == "__main__":
# No.J58II 左旋转字符串
s = SolutionJ58II()
in_put_1 = "abcdefg"
in_put_2 = 2
result = s.reverseLeftWords(in_put_1, in_put_2)
print(result)4.1.6 实现strStr()(No.28)
题目描述
给你两个字符串
haystack和needle,请你在haystack字符串中找出needle字符串出现的第一个位置(下标从0开始)。如果不存在,则返回-1。当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
示例
输入:haystack = “hello”, needle = “ll”
输出:2
题解
- 字符串匹配
KMP算法
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配。- 前缀表:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
python中使用str.find()方法可以一行解决。- 时间复杂度:
O(n + m), 暴力解法为O(n * m)- 空间复杂度:
O(m), 暴力解法为O(1)
# No.28 实现strStr() 类型:字符串
class Solution28(object):
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
if len(needle) == 0:
return 0
# 前缀表
next_list = [0] * len(needle) # 前缀表的值即为当前子串的最大相同前后缀长度
j = 0 # i指向后缀开头,j指向前缀开头
for i in range(1, len(needle)): # 从1开始!
while j > 0 and needle[i] != needle[j]: # 若不等,则往前回退一步
j = next_list[j - 1]
if needle[i] == needle[j]:
j += 1
next_list[i] = j
# 匹配过程
n = 0 # m指向haystack,n指向needle
for m in range(len(haystack)):
while n > 0 and haystack[m] != needle[n]:
n = next_list[n - 1]
if haystack[m] == needle[n]:
n += 1
if n == len(needle):
return m - len(needle) + 1
return -1
# OneLine
# return haystack.find(needle)
if __name__ == "__main__":
# No.28 实现strStr()
s = Solution28()
in_put_1 = "hello"
in_put_2 = "ll"
result = s.strStr(in_put_1, in_put_2)
print(result)4.1.7 重复的子字符串(No.359)
题目描述
给定一个非空的字符串,判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母,并且长度不超过10000。
示例
输入: “abab”
输出: True
解释: 可由子字符串 “ab” 重复两次构成。
题解
- 若一个字符串可由其子串重复多次构成
<=>该字符串的最长相同前后缀%(字符串长度-该字符串的最长相同前后缀)==0- 因此使用
KMP算法求得该字符串的前缀表即可。- 时间复杂度:
O(n)- 空间复杂度:
O(n)
# No.359 重复的子字符串 类型:字符串
class Solution359(object):
def repeatedSubstringPattern(self, s):
"""
:type s: str
:rtype: bool
"""
j = 0
next_list = [0] * len(s)
for i in range(1, len(s)):
while j > 0 and s[j] != s[i]:
j = next_list[j - 1]
if s[j] == s[i]:
j += 1
next_list[i] = j
# 重复字串str*n, 则最长相同前后缀为str*(n-1),因此必有str*(n-1) % (str*n - str*(n-1)) == 0
if next_list[-1] != 0 and next_list[-1] % (len(s) - next_list[-1]) == 0:
return True
else:
return False
if __name__ == "__main__":
# No.359 重复的子字符串
s = Solution359()
in_put = 'ababac'
result = s.repeatedSubstringPattern(in_put)
print(result)4.1.8 最长不含重复字符的子字符串(No.JZ48)
class SolutionJZ48(object):
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
if len(s) <= 1:
return len(s)
# 动态规划
# dp = [0] * len(s)
# dp[0] = 1
# d = {s[0]:0}
# for i in range(1,len(s)):
# if s[i] in d:
# idx = d[s[i]]
# else:
# idx = -1
# d[s[i]] = i
# if i - idx > dp[i-1]:
# dp[i] = dp[i-1] + 1
# else:
# dp[i] = i - idx
# return max(dp)
# 滑动窗口(双指针)
res = 0
d = dict()
i = 0 # i,j 为窗口的左右边界
for j in range(len(s)):
if s[j] in d:
i = max(d[s[j]]+1, i)
d[s[j]] = j
res = max(res, j - i + 1)
return res4.1.9 把字符串转换成整数(No.JZ67)
class SolutionJZ67:
def strToInt(self, str: str) -> int:
if not str: return 0
res,i,n,sign = 0,0,len(str),1
int_min, int_max, b = -2**31, 2**31-1, 2**31//10
# 处理空格
while str[i]==' ':
i += 1
if i==n: return 0 # 全是空格,直接返回
# 判断符号
if str[i] == '-': sign = -1
if str[i] in '+-': i += 1
while i < n and '9'>=str[i]>='0':
# 处理越界
if res > b or (res==b and str[i]>'7'):
return int_max if sign==1 else int_min
# 计算数值
res = 10*res + ord(str[i])-ord('0')
i += 1
return sign * res4.1.10 表示数值的字符串(No.JZ20)
class SolutionJZ20:
def isNumber(self, s: str) -> bool:
hasnum,hasdot,hase,hassign = False,False,False,False
idx,n = 0,len(s)
while s[idx] == ' ':
idx += 1
if idx == n:
return False
while idx < n:
# 如果当前字符c是数字:将hasNum置为true,index往后移动一直到非数字或遍历到末尾位置;如果已遍历到末尾(index == n),结束循环
while idx < n and '9'>=s[idx]>='0':
idx += 1
hasnum = True
if idx == n:
break
# 如果当前字符c是'e'或'E':如果e已经出现或者当前e之前没有出现过数字,返回fasle;否则令hasE = true,并且将其他3个flag全部置为false,因为要开始遍历e后面的新数字了
if s[idx] in ('e','E'):
if hase or not hasnum:
return False
else:
hase = True
hasnum,hasdot,hassign = False,False,False
# 如果当前字符c是+或-:如果已经出现过+或-或者已经出现过数字或者已经出现过'.',返回flase;否则令hasSign = true
elif s[idx] in ('+', '-'):
if hassign or hasnum or hasdot:
return False
else:
hassign = True
# 如果当前字符c是'.':如果已经出现过'.'或者已经出现过'e'或'E',返回false;否则令hasDot = true
elif s[idx] == '.':
if hasdot or hase:
return False
else:
hasdot = True
elif s[idx] == ' ':
break
else:
return False
idx += 1
while idx < n and s[idx] == ' ':
idx += 1
return hasnum and idx==n4.1.11 字符串相加(No.415)
class Solution415:
def addStrings(self, num1: str, num2: str) -> str:
# 双指针模拟加法
res = ''
i,j = len(num1)-1,len(num2)-1
jinwei = 0
while i>=0 or j>=0:
if i < 0:
s = int(num2[j]) + jinwei
elif j < 0:
s = int(num1[i]) + jinwei
else:
s = int(num1[i]) + int(num2[j]) + jinwei
ans = s % 10
jinwei = s // 10
res = str(ans) + res
i -= 1
j -= 1
return res if not jinwei else '1'+res4.1.12 字符串相乘(No.43)
class Solution:
def multiply(self, num1: str, num2: str) -> str:
# 模拟乘法
l1,l2 = len(num1),len(num2)
j = l2 - 1
res = 0
while j >= 0:
jinwei = 0
res_j = 0
for i in range(l1-1,-1,-1):
ans = int(num1[i]) * int(num2[j]) + jinwei
digit = ans % 10
jinwei = ans // 10
res_j += digit*(10)**(l1-1-i)
if jinwei > 0:
res_j += jinwei*10**l1
res += res_j*10**(l2-1-j)
j -= 1
return str(res)4.1.13 最短回文串(No.214)
class Solution214:
def shortestPalindrome(self, s: str) -> str:
n = len(s)
if n <= 1:
return s
# 暴力法,先翻转,删除s和rev_s重复的部分,再返回
# rev_s = s[::-1]
# for i in range(n):
# if s[:n-i] == rev_s[i:]:
# return rev_s[:i] + s
# KMP算法,求s#rev_s的最长公共前后缀,此即为以s[0]开头的最长回文子串
rev_s = s[::-1]
target_s = s + '#' + rev_s
n = len(target_s)
next_list = [0] * n # 前缀表
j = 0
for i in range(1,n):
while j > 0 and target_s[i] != target_s[j]:
j = next_list[j-1]
if target_s[i] == target_s[j]:
j += 1
next_list[i] = j
length = next_list[-1]
return s[length:][::-1] + s4.1.14 最小覆盖子串(No.76)
class Solution:
def minWindow(self, s: str, t: str) -> str:
# 滑动窗口
# 字典保存t中字符需要的次数,cnt为总的需要次数
dic = dict()
cnt = len(t)
for char in t:
if char not in dic:
dic[char] = 0
dic[char] += 1
j = 0
left, right = 0,len(s) # 保存结果
flag = False
for i in range(len(s)):
if s[i] not in dic: # 如果左边界字符不在t中,继续
continue
while cnt>0 and j < len(s): # 不断移动右边界直到找到所有t中字符
if s[j] in dic:
dic[s[j]] -= 1
if dic[s[j]] >= 0:
cnt -= 1
j += 1
if cnt > 0: # j到末尾了仍不满足,退出循环
break
if j - i <= right - left: # 更新最小区间
flag = True
right = j
left = i
dic[s[i]] += 1 # i右移一步,释放了1个有效字符
if dic[s[i]] > 0:
cnt += 1
return s[left:right] if flag else ""4.1.15 比较版本号(No.165)
class Solution165:
def compareVersion(self, version1: str, version2: str) -> int:
# 字符串分割再逐位比较
s1 = version1.split('.')
s2 = version2.split('.')
i,j = 0,0
while i<len(s1) or j<len(s2):
if i >= len(s1):
num1 = 0
else:
num1 = int(s1[i])
if j >= len(s2):
num2 = 0
else:
num2 = int(s2[j])
if num1 > num2:
return 1
elif num1 < num2:
return -1
else:
i += 1
j += 1
return 04.2 典型例题
4.2.1 最长公共前缀(No.14)
class Solution14:
def longestCommonPrefix(self, strs: List[str]) -> str:
# 取第一个字符串与后续字符串取前缀
s1 = strs[0]
for i in range(1,len(strs)):
s2 = strs[i]
idx = 0
while idx<len(s1) and idx<len(s2) and s1[idx] == s2[idx]:
idx += 1
s1 = s1[:idx] # 将待比较的字符串更新为公共前缀
return s14.2.2 面试题01.06.字符串压缩
class Solution0106:
def compressString(self, S: str) -> str:
# 双指针
if len(S) <= 2:
return S
left = 0
res = ''
for right in range(1,len(S)+1):
if right == len(S) or S[left] != S[right]:
res += S[left] + str(right-left)
left = right
return res if len(res) < len(S) else S<Paste>4.2.3 压缩字符串(No.443)
class Solution443:
def compress(self, chars: List[str]) -> int:
left,ans = 0,0
# 三指针,ans用来更新结果
for right in range(len(chars)+1):
if right==len(chars) or chars[left] != chars[right]:
chars[ans] = chars[left]
if right - left > 1:
s = str(right-left)
for i,c in enumerate(s):
chars[ans+i+1] = c
ans += len(s)+1
else:
ans += 1
left = right
return ans4.2.4 Z字形变换(No.6)
class Solution:
def convert(self, s: str, numRows: int) -> str:
# 按行处理,确定规律
if len(s) == 1 or numRows==1:
return s
res = []
dis = numRows + numRows - 2
for i in range(numRows):
idx = i
if i == 0 or i == numRows-1:
while idx < len(s):
res.append(s[idx])
idx += dis
else:
while idx < len(s):
res.append(s[idx])
if idx+dis-2*i < len(s):
res.append(s[idx+dis-2*i])
idx += dis
return ''.join(res)
# 模拟行索引变化
if numRows < 2:
return s
res = [""] * numRows
flag = -1
i = 0
for c in s:
res[i] += c
if i==0 or i==numRows-1:
flag = -flag
i += flag
return ''.join(res)5. 动态规划
5.1 典型例题
5.1.1 编辑距离(No.72)
class Solution72(object):
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
# 暴力递归
# def dp(i, j):
# if i == -1:
# return j + 1
# if j == -1:
# return i + 1
# if word1[i] == word2[j]:
# return dp(i -1, j - 1)
# else:
# return min(dp(i, j -1)+1, dp(i - 1, j)+1, dp (i - 1, j - 1)+1)
# return dp(len(word1) - 1, len(word2) - 1)
# db table
db = [[0] * (len(word1)+1) for _ in range(len(word2)+1)]
for i in range(len(word1)+1):
db[0][i] = i
for j in range(len(word2)+1):
db[j][0] = j
for i in range(1,len(word2)+1):
for j in range(1,len(word1)+1):
if word1[j-1] == word2[i-1]:
db[i][j] = db[i-1][j-1]
else:
db[i][j] = min(db[i][j-1]+1,db[i-1][j]+1,db[i-1][j-1]+1)
return db[-1][-1]5.1.2 斐波那契数列(No.JZ10-I)
class SolutionJZ10-I(object):
def fib(self, n):
"""
:type n: int
:rtype: int
"""
# dp
if n<=1:
return n
dp = [0] * (n+1)
dp[1] = 1
for i in range(2,n+1):
dp[i] = dp[i-1]+dp[i-2]
# 需整数取模,浮点数会有误差
return dp[n] if dp[n] < 1000000007 else int(dp[n]%(1000000007))
# 递归 直接超时
# if n<=1:
# return n
# return self.fib(n-1)+self.fib(n-2)5.1.3 青蛙跳台阶问题(No.JZ10-II)
class SolutionJZ10-II(object):
def numWays(self, n):
"""
:type n: int
:rtype: int
"""
if n == 0:
return 1
if n==1 or n==2:
return n
dp = [0] * (n+1)
dp[1], dp[2] = 1,2
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n] % 10000000075.1.4 机器人的运动范围(No.JZ13)
class Solution(object):
def movingCount(self, m, n, k):
"""
:type m: int
:type n: int
:type k: int
:rtype: int
"""
# DP 是否可达
# dp = [[0]*n for _ in range(m)]
# dp[0][0] = 1
# for i in range(m):
# for j in range(n):
# if digitsum(i)+digitsum(j)>k:
# continue
# if i>0 and j>0:
# dp[i][j] = dp[i-1][j] or dp[i][j-1]
# elif i>0 and j==0:
# dp[i][j] = dp[i-1][j]
# elif i==0 and j>0:
# dp[i][j] = dp[i][j-1]
# res = 0
# for i in range(m):
# res += sum(dp[i])
# return res
# DFS
# def dfs(i,j):
# if i>=m or j>=n or (digitsum(i)+digitsum(j)>k) or (i,j) in visited:
# return 0
# visited.add((i,j))
# return 1 + dfs(i+1,j) + dfs(i,j+1)
# visited = set()
# return dfs(0,0)
# BFS
quene, visited = [(0,0)], set()
while quene:
i,j = quene[0]
quene.pop(0)
if i>=m or j >=n or (digitsum(i)+digitsum(j)>k) or (i,j) in visited:
continue
visited.add((i,j))
quene.append((i+1,j))
quene.append((i,j+1))
return len(visited)
# 计算数位之和
def digitsum(n):
res = 0
while n:
res += n % 10
n //= 10
return res5.1.5 丑数(No.JZ49)
class SolutionJZ49(object):
def nthUglyNumber(self, n):
"""
:type n: int
:rtype: int
"""
dp = [0]*n
dp[0] = 1
a,b,c = 0,0,0
for i in range(1,n):
dp[i] = min(dp[a]*2,dp[b]*3,dp[c]*5)
# 此处if不能互斥,不能使用elif
if dp[i] == dp[a]*2:
a += 1
if dp[i] == dp[b]*3:
b += 1
if dp[i] == dp[c]*5:
c += 1
return dp[-1]5.1.6 不同路径(No.62)
class Solution62(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
dp = [[0]*n for _ in range(m)]
for i in range(m):
for j in range(n):
if i==0 or j==0:
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]5.1.7 最小路径和(No.64)
class Solution64(object):
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
m = len(grid)
n = len(grid[0])
dp = [[0]*n for _ in range(m)]
for i in range(m):
for j in range(n):
if i!=0 and j!=0:
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
elif i==0 and j!=0:
dp[i][j] = dp[i][j-1] + grid[i][j]
elif i!=0 and j==0:
dp[i][j] = dp[i-1][j] + grid[i][j]
elif i==0 and j==0:
dp[i][j] = grid[i][j]
return dp[-1][-1]
# 一维dp
# m,n = len(grid), len(grid[0])
# dp = [0]*n
# dp[0] = grid[0][0]
# 初始化
# for i in range(1,n):
# dp[i] = dp[i-1] + grid[0][i]
# for i in range(1,m):
# for j in range(n):
# if j > 0:
# dp[j] = min(dp[j-1],dp[j]) + grid[i][j]
# else:
# dp[j] = dp[j] + grid[i][j]5.1.8 剪绳子(No.JZ14-I)
class SolutionJZ14-I(object):
def cuttingRope(self, n):
"""
:type n: int
:rtype: int
"""
# 贪心思想
# if n==2 or n==3:
# return n-1
# res = 1
# 分段结果必是若干个3和2的组合,且优先3的数量
# while n%3:
# n -= 2
# res *= 2
# return res*3**(n/3)
# dp
dp = [0]*(n+1)
dp[2] = 1
for i in range(3,n+1):
for j in range(2,i):
dp[i] = max(dp[i], max(j*dp[i-j], j*(i-j)))
return dp[-1]5.1.9 剪绳子II(No.JZ14-II)
class SolutionJZ14-II(object):
def cuttingRope(self, n):
"""
:type n: int
:rtype: int
"""
if n==2 or n==3:
return n-1
a, b = n//3, n%3
if b==0:
return (3**a)%1000000007
elif b==1:
return (3**(a-1)*4)%1000000007
else:
return (3**a*2)%10000000075.1.10 连续子数组的最大和(No.JZ42)
class SolutionJZ42(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# dp[i]表示以nums[i]结尾的连续子数组最大值
dp = [0]*len(nums)
dp[0] = nums[0]
for i in range(1,len(nums)):
if dp[i-1]<=0:
dp[i] = nums[i]
else:
dp[i] = dp[i-1] + nums[i]
return max(dp)5.1.11 把数字翻译成字符串(No.JZ46)
class SolutionJZ46(object):
def translateNum(self, num):
"""
:type num: int
:rtype: int
"""
num = str(num)
if len(num)==1:
return 1
# dp = [0]*len(num)
# dp[0] = 1
# dp[1] = 1 if num[:2]>'25' else 2
# for i in range(2,len(num)):
# if num[i-1]+num[i]>'25' or num[i-1]+num[i]<'10':
# dp[i] = dp[i-1]
# else:
# dp[i] = dp[i-1] + dp[i-2]
# return dp[-1]
# 空间优化
a, b = 1,1
for i in range(2, len(num)+1):
if '25'>=num[i-2:i]>='10':
a,b = a+b,a
else:
b = a
return a5.1.12 礼物的最大价值(No.JZ47)
class Solution(object):
def maxValue(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
m = len(grid)
n = len(grid[0])
dp = [[0]*n for _ in range(m)]
for i in range(m):
for j in range(n):
if i==0 and j==0:
dp[i][j] = grid[i][j]
elif i==0 and j!=0:
dp[i][j] = dp[i][j-1] + grid[i][j]
elif i!=0 and j==0:
dp[i][j] = dp[i-1][j] + grid[i][j]
else:
dp[i][j] = max(dp[i-1][j],dp[i][j-1])+grid[i][j]
return dp[-1][-1]5.1.13 n个骰子的点数(No.JZ60)
class SolutionJZ60:
def dicesProbability(self, n: int) -> List[float]:
# 两个一维数组交替
dp = [1/6] * 6
temp = [0] * (len(dp)+5)
while len(dp)!= (5*n+1):
for i in range(len(dp)):
# 只能影响6位
for j in range(6):
temp[i+j] += dp[i]*(1/6)
dp = temp
temp = [0] * (len(dp)+5)
return dp5.1.14 股票的最大利润(No.JZ63)
class SolutionJZ63(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if prices==[]:
return 0
dp = [0]*len(prices)
dp[0] = 0
# 用一个变量来记录最小值,可降低时间复杂度
min_cost = prices[0]
for i in range(1,len(prices)):
dp[i] = max(dp[i-1],prices[i]-min_cost)
min_cost = min(min_cost, prices[i])
return dp[-1]5.1.15 正则表达式匹配(No.JZ19)
class SolutionJZ19(object):
def isMatch(self, s, p):
"""
:type s: str
:type p: str
:rtype: bool
"""
m = len(s)+1
n = len(p)+1
dp = [[False]*n for _ in range(m)]
for i in range(m):
for j in range(n):
if j==0:
if i==0:
dp[i][j] = True
else:
if p[j-1] != '*':
if i>0 and (s[i-1]==p[j-1] or p[j-1]=='.'):
dp[i][j] = dp[i-1][j-1]
else:
if j>=2:
dp[i][j] |= dp[i][j-2]
if i>0 and j>=2 and (s[i-1]==p[j-2] or p[j-2]=='.'):
dp[i][j] |= dp[i-1][j]
return dp[-1][-1]5.1.16 最长递增子序列(No.300)
class Solution300(object):
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums)==1:
return 1
dp = [1] * len(nums)
for i in range(1,len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j]+1)
return max(dp)5.1.17 最长递增子序列的个数(No.673)
class Solution673:
def findNumberOfLIS(self, nums: List[int]) -> int:
# 动态规划 dp[i]表示以nums[i]结尾的最长递增子序列的长度,cnt[i]表示对应的次数
n,res = len(nums),0
dp = [1] * n
cnt = [1] * n
for i in range(1,n):
for j in range(i):
if nums[i] > nums[j]:
if dp[j] + 1 > dp[i]:
dp[i] = dp[j] + 1
cnt[i] = cnt[j]
elif dp[j] + 1 == dp[i]:
cnt[i] += cnt[j]
longest = max(dp)
for i in range(n):
if dp[i] == longest:
res += cnt[i]
return res5.1.18 圆圈中最后剩下的数字(No.JZ62)
class SolutionJZ62(object):
def lastRemaining(self, n, m):
"""
:type n: int
:type m: int
:rtype: int
"""
# 约瑟夫环问题
# 暴力法超时
# nums = [i for i in range(n)]
# pre = 0
# while len(nums) > 1:
# idx = (pre + m -1) % len(nums)
# nums.pop(idx)
# pre = idx
# return nums[0]
# 动态规划
dp = [0] * (n+1)
for i in range(2,n+1):
dp[i] = (dp[i-1]+m)%i
return dp[-1]5.1.19 最长回文子串(No.5)
class Solution5:
def longestPalindrome(self, s: str) -> str:
# 动态规划 dp[i][j] 表示是否s[i:j+1]为回文字符串
n = len(s)
dp = [[0]*n for _ in range(n)]
for i in range(n):
dp[i][i] = 1
left, right = 0, 0
for i in range(n-1,-1,-1):
for j in range(i+1,n):
# 状态转移,要考虑偶数个字符如'bb'的情况
if s[i] == s[j]:
if dp[i+1][j-1] == 1 or j - i == 1:
dp[i][j] = 1
if j-i > right-left:
left,right = i,j
return s[left:right+1]5.1.20 最长回文子序列(No.516)
class Solution516:
def longestPalindromeSubseq(self, s: str) -> int:
# 动态规划 dp[i][j]表示s[i:j+1]中最长回文子序列的长度
n = len(s)
dp = [[0]*n for _ in range(n)]
for i in range(n):
dp[i][i] = 1
for i in range(n-1,-1,-1):
for j in range(i+1,n):
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i][j-1],dp[i+1][j])
return dp[0][-1]5.1.21 买卖股票的最佳时机II(No.122)
class Solution122:
def maxProfit(self, prices: List[int]) -> int:
# 贪心算法
# res = 0
# for i in range(1,len(prices)):
# if prices[i] > prices[i-1]:
# res += prices[i]-prices[i-1]
# return res
# 动态规划, dp[i][j] 表示到下标为 i 的这一天,持股状态为 j 时,我们手上拥有的最大现金数。0为不持股,1为持股
dp = [[0]*2 for _ in range(len(prices))]
dp[0][1] = -prices[0]
for i in range(1,len(prices)):
dp[i][0] = max(dp[i-1][0],dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0] - prices[i])
return dp[-1][0]5.1.22 买卖股票的最佳时机III(No.123)
class Solution123:
def maxProfit(self, prices: List[int]) -> int:
# 动态规划,每一天有五种股票状态,无操作、第一次买入、第一次卖出、第二次买入、第二次卖出
# n = len(prices)
# dp = [[0]*5 for _ in range(n)]
# dp[0][0] = 0
# dp[0][1] = -prices[0]
# dp[0][2] = 0
# dp[0][3] = -prices[0]
# dp[0][4] = 0
# for i in range(1,n):
# dp[i][0] = dp[i-1][0]
# dp[i][1] = max(dp[i-1][0]-prices[i], dp[i-1][1])
# dp[i][2] = max(dp[i-1][1]+prices[i], dp[i-1][2])
# dp[i][3] = max(dp[i-1][2]-prices[i], dp[i-1][3])
# dp[i][4] = max(dp[i-1][3]+prices[i], dp[i-1][4])
# return dp[-1][-1]
# 空间优化
n = len(prices)
buy1,buy2 = -prices[0],-prices[0]
sell1,sell2 = 0,0
for i in range(1,n):
buy1 = max(buy1, -prices[i])
sell1 = max(sell1, buy1 + prices[i])
buy2 = max(buy2, sell1 - prices[i])
sell2 = max(sell2, buy2 + prices[i])
return sell25.1.23 买卖股票的最佳时机IV(No.188)
class Solution188:
def maxProfit(self, k: int, prices: List[int]) -> int:
if not prices or k==0:
return 0
# 动态规划
dp = [0] * k * 2
for i in range(len(dp)):
if i % 2 == 0:
dp[i] = -prices[0]
n = len(prices)
for i in range(1,n):
for j in range(len(dp)):
if j == 0:
dp[j] = max(dp[j], -prices[i])
elif j % 2 == 1:
dp[j] = max(dp[j], dp[j-1] + prices[i])
else:
dp[j] = max(dp[j], dp[j-1] - prices[i])
return dp[-1]5.1.24 最佳买卖股票时机含冷冻期(No.309)
class Solution309:
def maxProfit(self, prices: List[int]) -> int:
# 动态规划, 0不持股非冷冻期,1持股,2不持股冷冻期(第i天结束后为冷冻期)
n = len(prices)
dp = [[0]*3 for _ in range(n)]
dp[0][0] = 0
dp[0][1] = -prices[0]
dp[0][2] = 0
for i in range(1,n):
dp[i][0] = max(dp[i-1][0], dp[i-1][2])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
dp[i][2] = dp[i-1][1] + prices[i]
return max(dp[-1][0],dp[-1][2])5.1.25 最大正方形(No.221)
class Solution221:
def maximalSquare(self, matrix: List[List[str]]) -> int:
# 动态规划, dp[i][j]代表以matrix[i][j]为右下点的矩阵的最大边长
m,n = len(matrix), len(matrix[0])
dp = [[0]*n for _ in range(m)]
for i in range(m):
if matrix[i][0]=='1':
dp[i][0] = 1
for i in range(n):
if matrix[0][i]=='1':
dp[0][i] = 1
for i in range(1,m):
for j in range(1,n):
if matrix[i][j]=='0':
dp[i][j] = 0
else:
dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) + 1
return max([max(i) for i in dp]) ** 25.2 典型例题
5.2.1 构建乘积数组(No.JZ66)
class Solution:
def constructArr(self, a: List[int]) -> List[int]:
# 不允许用除法
# 暴力法超时
# res = []
# for i in range(len(a)):
# temp = 1
# for j in range(len(a)):
# if j == i:
# continue
# temp *= a[j]
# res.append(temp)
# return res
# 动态规划,维护左右两个数组
n = len(a)
dp_l = [1] * n
dp_r = [1] * n
for i in range(1,n):
dp_l[i] = dp_l[i-1] * a[i-1]
dp_r[-i - 1] = dp_r[-i] * a[-i]
res = []
for i in range(n):
res.append(dp_l[i]*dp_r[i])
return res5.2.2 最长重复子数组(No.718)
class Solution718:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
# 动态规划 dp[i][j] 表示以nums1[i]结尾、nums2[j]结尾的字符串的公共子数组最大长度
m,n = len(nums1), len(nums2)
dp = [[0]*n for _ in range(m)]
for i in range(m):
if nums1[i] == nums2[0]:
dp[i][0] = 1
for i in range(n):
if nums2[i] == nums1[0]:
dp[0][i] = 1
for i in range(1,m):
for j in range(1,n):
if nums1[i] == nums2[j]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = 0
res = 0
for i in dp:
res = max(res, max(i))
return res5.2.3 最长公共子序列(No.1143)
class Solution1143:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
# 动态规划 dp[i][j]表示text1[:i+1] text2[:j+1]字符串的最长公共子序列
l1,l2 = len(text1),len(text2)
dp = [[0]*l2 for _ in range(l1)]
if text1[0] == text2[0]:
dp[0][0] = 1
for i in range(1,l1):
if dp[i-1][0] == 1 or text1[i] == text2[0]:
dp[i][0] = 1
for i in range(1,l2):
if dp[0][i-1] == 1 or text2[i] == text1[0]:
dp[0][i] = 1
for i in range(1,l1):
for j in range(1,l2):
if text1[i] == text2[j]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
return dp[-1][-1]5.2.4 最大的以 1 为边界的正方形(No.1139)
class Solution1139:
def largest1BorderedSquare(self, grid: List[List[int]]) -> int:
# 暴力法
def is_matrix(x,y,n):
for i in range(n):
if grid[x][y+i] == 0:
return 0
for i in range(n):
if grid[x+n-1][y+i] == 0:
return 0
for i in range(n):
if grid[x+i][y] == 0:
return 0
for i in range(n):
if grid[x+i][y+n-1] == 0:
return 0
return n**2
# m,n = len(grid), len(grid[0])
# res = 0
# for i in range(m):
# for j in range(n):
# l_range = min(m-i,n-j)
# for k in range(l_range):
# res = max(res,is_matrix(i,j,k+1))
# return res
# 动态规划 dp_l[i][j]表示grid[i][j]左边连续1的个数, dp_t[i][j]表示grid[i][j]上边连续1的个数,都包括grid[i][j]本身
m,n = len(grid), len(grid[0])
dp_l = [[0] * n for _ in range(m)]
dp_t = [[0] * n for _ in range(m)]
if grid[0][0] == 1:
dp_l[0][0] = 1
dp_t[0][0] = 1
for i in range(1,m):
if grid[i][0] == 1:
dp_l[i][0] = 1
dp_t[i][0] = dp_t[i-1][0] + 1
for j in range(1,n):
if grid[0][j] == 1:
dp_l[0][j] = dp_l[0][j-1] + 1
dp_t[0][j] = 1
for i in range(1,m):
for j in range(1,n):
if grid[i][j] == 1:
dp_l[i][j] = dp_l[i][j-1] + 1
dp_t[i][j] = dp_t[i-1][j] + 1
res = 0
for i in range(m):
for j in range(n):
l_range = min(dp_l[i][j], dp_t[i][j])
for k in range(l_range):
if dp_t[i][j-k] >= k+1 and dp_l[i-k][j] >= k+1:
res = max(res, (k+1)**2)
return res5.2.5 分割回文串II(No.132)
class Solution132:
def minCut(self, s: str) -> int:
# 优化,动态规划求每个子串是否为回文串,dp[i][j]表示s[i:j+1]是否为回文串
n = len(s)
dp = [[False]*n for _ in range(n)]
for i in range(n):
dp[i][i] = True
for i in range(n-1,-1,-1):
for j in range(i+1,n):
dp[i][j] = s[i] == s[j] and (dp[i+1][j-1] or j-i==1)
# dp_s[i]表示以第i个字符结尾的子串的最少分割次数
dp_s = [n] * (n+1)
dp_s[0] = 0
for i in range(1,n+1):
if dp[0][i-1]: # 若整个子串是回文串,则0次分割
dp_s[i] = 0
else:
for left in range(2,i+1): # 不断调整子串的左边界,取最小
if dp[left-1][i-1]:
dp_s[i] = min(dp_s[i], dp_s[left-1]+1)
return dp_s[-1]5.2.6 打家劫舍(No.198)
class Solution198:
def rob(self, nums: List[int]) -> int:
# 动态规划 0表示偷,1表示不能偷,2表示能偷但不偷
# n = len(nums)
# dp = [[0]*3 for _ in range(n)]
# dp[0][0] = nums[0]
# dp[0][1] = 0
# dp[0][2] = 0
# for i in range(1,n):
# dp[i][0] = max(dp[i-1][1],dp[i-1][2]) + nums[i]
# dp[i][1] = dp[i-1][0]
# dp[i][2] = max(dp[i-1][1], dp[i-1][2])
# return max(dp[-1][0], dp[-1][1], dp[-1][2])
n = len(nums)
if n == 1:
return nums[0]
dp = [0] * n
dp[0] = nums[0]
dp[1] = max(nums[0],nums[1])
for i in range(2,n):
dp[i] = max(dp[i-1], dp[i-2]+nums[i]) # 第i间偷不偷
return dp[-1]5.2.7 打家劫舍II(No.213)
class Solution:
def rob(self, nums: List[int]) -> int:
# 动态规划, 环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃
# 分别对这两种情况计算,取最大
def my_dp(nums):
n = len(nums)
if n == 1:
return nums[0]
dp = [0] * n
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2,n):
dp[i] = max(dp[i-1],dp[i-2]+nums[i])
return dp[-1]
if len(nums) == 1:
return nums[0]
return max(my_dp(nums[:-1]),my_dp(nums[1:]))5.2.8 打家劫舍III(No.337)
class Solution337:
def rob(self, root: TreeNode) -> int:
# 暴力递归超时,使用哈希表存储结果
def recur(root):
if not root:
return 0
if root in dic:
return dic[root]
money = root.val
if root.left:
money += recur(root.left.left) + recur(root.left.right)
if root.right:
money += recur(root.right.left) + recur(root.right.right)
res = max(money, recur(root.left) + recur(root.right))
dic[root] = res
return res
# dic = dict()
# return recur(root)
# 动态规划
def my_dp(root):
if not root:
return [0,0]
left = my_dp(root.left)
right = my_dp(root.right)
dp = [0,0]
# dp[0]表示以当前节点不偷状态下子树能够偷取的最大值,注意当前节点不偷的话,它的子树可以偷也可以不偷
dp[0] = max(left[0],left[1]) + max(right[0],right[1])
# dp[1]表示当前节点偷状态下子树能够偷取的最大值
dp[1] = root.val + left[0] + right[0]
return dp
res = my_dp(root)
return max(res[0],res[1])5.2.9 最长有效括号(No.32)
class Solution32:
def longestValidParentheses(self, s: str) -> int:
# 动态规划dp[i]表示以s[i]结尾的字符串最长有效括号子串的长度
dp = [0] * len(s)
res = 0
for i in range(1,len(s)):
if s[i] == '(':
dp[i] = 0
else:
if s[i-1] == '(':
dp[i] = dp[i-2]+2 if i-2>=0 else 2
else:
if i-dp[i-1]-1<0 or s[i-dp[i-1]-1] == ')':
dp[i] = 0
else:
dp[i] = dp[i-dp[i-1]-2] + dp[i-1] + 2 if i-dp[i-1]-2>=0 else dp[i-1] + 2
res = max(res,dp[i])
return res5.3 背包问题
5.3.1 分割等和子集(No.416)
class Solution416:
def canPartition(self, nums: List[int]) -> bool:
# 转化为01背包问题:是否可以从输入数组中挑选出一些正整数,使得这些数的和等于整个数组元素的和的一半
# dp[i][j] 表示nums[:i+1]中能否找到一些数,使得它们的和等于j
sum_nums = sum(nums)
if not sum_nums % 2 == 0:
return False
n, target = len(nums), int(sum_nums / 2)
# dp = [[False]*(target+1) for _ in range(n)]
# for j in range(target+1):
# if j == nums[0]:
# dp[0][j] = True
# break
# for i in range(1,n):
# for j in range(target+1):
# if j < nums[i]:
# dp[i][j] = dp[i-1][j]
# else:
# dp[i][j] = dp[i-1][j] or dp[i-1][j-nums[i]]
# if dp[i][j]: return True # 只要某行最后一列为True,后续行最后一列也都为True
# return dp[-1][-1]
# 空间优化,一维dp[j]表示能否使得和为j
dp = [False] * (target + 1)
if nums[0] <= target:
dp[nums[0]] = True
for i in range(1,n):
for j in range(target, -1, -1):
if j >= nums[i]:
dp[j] = dp[j] or dp[j-nums[i]]
else:
break
if dp[-1]: return True
return dp[-1]5.3.2 一和零(No.474)
class Solution474:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
# 多维01背包问题,dp[i][j][k]表示strs[:i+1]中最多j个0k个1的最大子集大小
num_0, num_1 = [], []
for s in strs:
n_0 = 0
n_1 = 0
for char in s:
if char == '0':
n_0 += 1
else:
n_1 += 1
num_0.append(n_0)
num_1.append(n_1)
length = len(strs)
dp = [[[0]*(n+1) for _ in range(m+1)] for _ in range(length)]
# 初始化第一行(处理第一个物体)
for j in range(m+1):
for k in range(n+1):
if j >= num_0[0] and k >= num_1[0]:
dp[0][j][k] = 1
for i in range(1,length):
for j in range(m+1):
for k in range(n+1):
if j >= num_0[i] and k >= num_1[i]:
dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-num_0[i]][k-num_1[i]]+1) # 状态转移,与一维01背包类似
else:
dp[i][j][k] = dp[i-1][j][k]
return dp[-1][-1][-1]5.3.3 目标和(No.494)
class Solution494:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
# 暴力dfs,超时,时间复杂度O(2^n)
def dfs(idx,cur):
if idx == len(nums):
return 1 if cur == target else 0
left = dfs(idx+1,cur+nums[idx])
right = dfs(idx+1,cur-nums[idx])
return left + right
# return dfs(0,0)
# 记忆化搜索,还是超时
def dfs_memo(idx,cur):
key = str(idx)+'_'+str(cur)
if key in cache: return cache[key]
if idx == len(nums):
cache[key] = 1 if cur == target else 0
return cache[key]
left = dfs(idx+1,cur+nums[idx])
right = dfs(idx+1,cur-nums[idx])
cache[key] = left + right
return left + right
# cache = dict()
# return dfs_memo(0,0)
# 动态规划,转化为01背包问题,假设所有符号为+的元素和为x,符号为-的元素和的绝对值是y。
# 则有target=x-y,sum = x+y,解得x = (target+sum)/2=新target
nums_sum = sum(nums)
if abs(target) > nums_sum or (target + nums_sum) % 2 != 0:
return 0
my_target = (target + nums_sum) // 2
dp = [0] * (my_target + 1)
dp[0] = 1 # 填满容量为0的背包有1种方法
for i in range(len(nums)):
for j in range(my_target, -1, -1):
if j >= nums[i]:
dp[j] = dp[j] + dp[j-nums[i]] # 状态转移
else:
break
return dp[-1]5.3.4 零钱兑换(No.322)
class Solution322:
def coinChange(self, coins: List[int], amount: int) -> int:
# 动态规划,完全背包,dp[j]为凑成总金额为j的最少硬币个数
m,n = len(coins), amount + 1
dp = [n] * n # 初始化为不可能达到的最大硬币数
dp[0] = 0 # 凑成金额为0需要0个硬币
for i in range(m):
for j in range(n):
if j >= coins[i]:
dp[j] = min(dp[j], dp[j-coins[i]]+1)
return dp[-1] if dp[-1] < n else -15.3.5 零钱兑换II(No.518)
class Solution518:
def change(self, amount: int, coins: List[int]) -> int:
# 动态规划,完全背包,dp[j]为凑成总金额j的硬币组合数
m,n = len(coins), amount+1
dp = [0] * n
dp[0] = 1
for i in range(m):
for j in range(n):
if j >= coins[i]:
dp[j] = dp[j] + dp[j-coins[i]] # 状态转移
return dp[-1]
# 二维dp
# dp = [[0]*n for _ in range(m+1)]
# dp[0][0] = 1
# for i in range(1,m+1):
# for j in range(n):
# if j >= coins[i-1]:
# dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]
# else:
# dp[i][j] = dp[i-1][j]
# return dp[-1][-1]5.3.6 组合总和Ⅳ(No.377)
class Solution377:
def combinationSum4(self, nums: List[int], target: int) -> int:
# 动态规划,完全背包,不同之处在于顺序不同的序列被视作不同的组合
m,n = len(nums), target + 1
dp = [0] * n
dp[0] = 1
# 交换遍历顺序,先物体后容量
for j in range(n):
for i in range(m):
if j >= nums[i]:
dp[j] = dp[j] + dp[j-nums[i]]
return dp[-1]6. 树
6.1 典型例题
6.1.1 从上到下打印二叉树(No.JZ32-I)
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class SolutionJZ32-I(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
# BFS
if not root:
return []
# quene = [root]
quene = collections.deque()
quene.append(root)
res = []
while quene:
node = quene.popleft() # list 的pop(0)时间复杂度为O(n), deque的为O(1)
res.append(node.val)
if node.left:
quene.append(node.left)
if node.right:
quene.append(node.right)
return res6.1.2 二叉树的层序遍历(No.102)
class Solution102(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return []
quene = [root]
res = []
while quene:
l = len(quene)
temp = []
for i in range(l):
node = quene.pop(0)
temp.append(node.val)
if node.left:
quene.append(node.left)
if node.right:
quene.append(node.right)
res.append(temp)
return res6.1.3 从上到下打印二叉树III(No.JZ32-III)
class SolutionJZ32-III(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return []
quene = [root]
res = []
flag = 1
while quene:
l = len(quene)
temp = []
flag += 1
for i in range(l):
node = quene.pop(0)
temp.append(node.val)
if node.left:
quene.append(node.left)
if node.right:
quene.append(node.right)
if flag%2:
temp = [temp[-1-i] for i in range(len(temp))]
res.append(temp)
return res6.1.4 二叉树的中序遍历(No.94)
class Solution94(object):
def inorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
res = []
self.inorder(root,res)
return res
# 迭代
# stack,res = [],[]
# while stack or root:
# if root:
# stack.append(root)
# root = root.left
# else:
# temp = stack.pop()
# res.append(temp.val)
# root = temp.right
# return res
def inorder(self,root, res):
if not root:
return
self.inorder(root.left, res)
res.append(root.val)
self.inorder(root.right,res)6.1.5 二叉树的前序遍历(No.144)
class Solution144(object):
def preorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
# res = []
# self.preorder(root,res)
# return res
# 迭代
if not root: return []
stack = [root]
res = []
while stack:
node = stack.pop()
res.append(node.val)
if node.right:
stack.append(node.right) # 栈的先入后出特性,因此要先右后左
if node.left:
stack.append(node.left)
return res
def preorder(self,root,res):
if not root:
return
res.append(root.val)
self.preorder(root.left,res)
self.preorder(root.right,res)6.1.6 二叉树的镜像(No.JZ27)
class SolutionJZ27(object):
def mirrorTree(self, root):
"""
:type root: TreeNode
:rtype: TreeNode
"""
if not root:
return
root.left, root.right = root.right, root.left
self.mirrorTree(root.left)
self.mirrorTree(root.right)
return root6.1.7 对称的二叉树(No.JZ28)
class SolutionJZ28(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
def recur(l,r):
if not l and not r:
return True
if not l or not r or l.val != r.val:
return False
return recur(l.left,r.right) and recur(l.right,r.left)
if not root:
return True
return recur(root.left,root.right)6.1.8 二叉树的深度(No.JZ55-I)
class SolutionJZ55-I(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root:
return 0
# BFS
# quene = [root]
# res = 0
# while quene:
# l = len(quene)
# for i in range(l):
# node = quene.pop(0)
# if node.left:
# quene.append(node.left)
# if node.right:
# quene.append(node.right)
# res += 1
# return res
# DFS
return max(self.maxDepth(root.left),self.maxDepth(root.right)) + 16.1.9 二叉搜索树的第k大节点(No.JZ54)
class SolutionJZ54(object):
def kthLargest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
def inorder(root):
if not root:
return
inorder(root.left)
self.res.append(root.val)
inorder(root.right)
self.res = []
inorder(root)
return self.res[-k]6.1.10 平衡二叉树(No.JZ55-II)
class SolutionJZ55-II(object):
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
# 前序遍历+计算深度
# def depth(root):
# if not root:
# return 0
# return max(depth(root.left),depth(root.right))+1
# def dfs(root):
# if not root:
# return True
# return abs(depth(root.left)-depth(root.right))<=1 and dfs(root.left) and dfs(root.right)
# return dfs(root)
# 后序遍历+剪枝
def recur(root):
if not root:
return 0
left = recur(root.left)
if left == -1:
return -1
right = recur(root.right)
if right == -1:
return -1
return max(left,right)+1 if abs(left-right)<=1 else -1
return recur(root) != -16.1.11 二叉搜索树的最近公共祖先(No.JZ68-I)
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
# 迭代,利用二插搜索树的性质,右子树>左子树
while root:
if p.val > root.val and q.val > root.val:
root = root.right
elif p.val < root.val and q.val < root.val:
root = root.left
else:
return root
# 递归
# if p.val > root.val and q.val > root.val:
# return self.lowestCommonAncestor(root.right,p,q)
# elif p.val < root.val and q.val < root.val:
# return self.lowestCommonAncestor(root.left,p,q)
# else:
# return root6.1.12 二叉树的最近公共祖先(No.JZ68-II)
class SolutionJZ68-II(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
if not root:
return
if root==p or root==q:
return root
left = self.lowestCommonAncestor(root.left,p,q)
right = self.lowestCommonAncestor(root.right,p,q)
if not left:
return right
if not right:
return left
return root6.1.13 重建二叉树(No.JZ7)
class SolutionJZ7(object):
def buildTree(self, preorder, inorder):
"""
:type preorder: List[int]
:type inorder: List[int]
:rtype: TreeNode
"""
# root代表根节点在前序遍历中的索引,left、right代表当前子树在中序遍历的左右边界
def recur(root,left,right):
if left > right:
return
node = TreeNode(preorder[root])
i = h[node.val]
node.left = recur(root+1,left,i-1)
node.right = recur(root+1+i-left,i+1,right)
return node
h = {}
for i,j in enumerate(inorder):
h[j] = i
return recur(0,0,len(inorder)-1)6.1.14 树的子结构(No.JZ26)
class SolutionJZ26(object):
def isSubStructure(self, A, B):
"""
:type A: TreeNode
:type B: TreeNode
:rtype: bool
"""
def recur(a,b):
if not b:
return True
if not a or a.val != b.val:
return False
return recur(a.left,b.left) and recur(a.right,b.right)
if not A or not B:
return False
return recur(A,B) or self.isSubStructure(A.left,B) or self.isSubStructure(A.right,B)6.1.15 二叉搜索树与双向链表(No.JZ36)
class SolutionJZ36(object):
def treeToDoublyList(self, root):
"""
:type root: Node
:rtype: Node
"""
def recur(root):
if not root:
return
recur(root.left)
if self.pre:
self.pre.right = root
else:
self.head = root
root.left = self.pre
self.pre = root
recur(root.right)
if not root:
return
self.pre = None
recur(root)
self.head.left, self.pre.right = self.pre,self.head
return self.head6.1.16 二叉搜索树的后序遍历序列(No.JZ33)
class SolutionJZ33(object):
def verifyPostorder(self, postorder):
"""
:type postorder: List[int]
:rtype: bool
"""
# 牢记二叉搜索树的性质,右子树>根节点的值>左子树
def recur(postorder):
if len(postorder)<=1:
return True
root = postorder[-1]
idx = len(postorder) - 1
for i in range(len(postorder)):
if postorder[i] > root:
idx = i
break
for j in postorder[idx:-1]:
if j < root:
return False
return recur(postorder[:idx]) and recur(postorder[idx:-1])
if not postorder:
return True
return recur(postorder)6.1.17 二叉树中和为某一值的路径(No.JZ34)
class SolutionJZ34(object):
def pathSum(self, root, target):
"""
:type root: TreeNode
:type target: int
:rtype: List[List[int]]
"""
def recur(root):
if not root:
return
self.sum += root.val
self.temp.append(root.val)
if not root.left and not root.right and self.sum == target:
# 注意list是可变对象,这里需要加list()复制一份,不然会动态变化
self.res.append(list(self.temp))
recur(root.left)
recur(root.right)
self.sum -= root.val
self.temp.pop()
self.res = []
self.temp = []
self.sum = 0
recur(root)
return self.res6.1.18 序列化二叉树(No.JZ37)
class Codec:
def serialize(self, root):
"""Encodes a tree to a single string.
:type root: TreeNode
:rtype: str
"""
if not root:
return '[]'
quene = [root]
res = []
while quene:
node = quene.pop(0)
if node:
res.append(str(node.val))
quene.append(node.left)
quene.append(node.right)
else:
res.append('null')
return '['+','.join(res)+']'
def deserialize(self, data):
"""Decodes your encoded data to tree.
:type data: str
:rtype: TreeNode
"""
if data == '[]':
return
nums = data[1:-1].split(',')
i = 1
root = TreeNode(int(nums[0]))
quene = [root]
while quene:
node = quene.pop(0)
if nums[i] != 'null':
node.left = TreeNode(int(nums[i]))
quene.append(node.left)
i += 1
if nums[i] != 'null':
node.right = TreeNode(int(nums[i]))
quene.append(node.right)
i += 1
return root6.1.19 二叉树的直径(No.543)
class Solution543:
def __init__(self):
self.res = 0
def diameterOfBinaryTree(self, root: TreeNode) -> int:
def dfs(root):
if not root:
return 0
left = dfs(root.left) # 左子树高度
right = dfs(root.right) # 右子树高度
self.res = max(self.res,(left + right)) # 更新最大值
return max(left, right) + 1 # 当前节点的高度
dfs(root)
return self.res6.1.20 二叉树的右视图(No.199)
class Solution199:
def rightSideView(self, root: TreeNode) -> List[int]:
# 层序遍历取最右边
if not root: return []
quene = [root]
res = []
while quene:
length = len(quene)
temp = []
for i in range(length):
node = quene.pop(0)
temp.append(node.val)
if node.left:
quene.append(node.left)
if node.right:
quene.append(node.right)
res.append(temp[-1])
# return res
# DFS 根--》右--》左
# def dfs(root, depth):
# if not root:
# return
# if len(res) == depth:
# res.append(root.val)
# depth += 1
# dfs(root.right, depth)
# dfs(root.left, depth)
# res = []
# dfs(root,0)
# return res6.2 典型例题
6.2.1 路径总和(No.112)
class Solution112:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
# DFS
def dfs(root,target):
if not root: return False
if not root.left and not root.right:
return target == root.val
target -= root.val
left = dfs(root.left, target)
right = dfs(root.right, target)
return left or right
return dfs(root,targetSum)6.2.2 路径总和II(No.113)
class Solution113:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
# 回溯
def dfs(root,target):
if not root:
return
path.append(root.val)
if not root.left and not root.right and target == root.val:
res.append(list(path))
dfs(root.left, target-root.val)
dfs(root.right, target-root.val)
path.pop()
res,path = [],[]
dfs(root,targetSum)
return res6.2.3 路径总和III(No.437)
class Solution437:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
# DFS
def dfs(root,target):
if not root:
return
if target - root.val == 0:
self.res += 1
dfs(root.left,target-root.val)
dfs(root.right,target-root.val)
# 遍历整个树
def preorder(root):
if not root:
return
dfs(root,targetSum)
preorder(root.left)
preorder(root.right)
# 双递归
self.res = 0
preorder(root)
return self.res6.2.4 求根节点到叶节点数字之和(No.129)
class Solution129:
def sumNumbers(self, root: TreeNode) -> int:
# 回溯
def dfs(root):
if not root:
return
path.append(root.val)
if not root.left and not root.right:
temp = 0
for num in path:
temp = temp*10 + num
self.res += temp
dfs(root.left)
dfs(root.right)
path.pop()
self.res,path = 0,[]
dfs(root)
return self.res6.2.5 验证二叉搜索树(No.98)
class Solution98:
def isValidBST(self, root: TreeNode) -> bool:
# 中序遍历,判断当前节点是否大于前节点
def recur(root):
if not root:
return True
left = recur(root.left)
if not left:
return False
if root.val <= self.pre:
return False
self.pre = root.val
return recur(root.right)
self.pre = float('-inf')
return recur(root)6.2.6 相同的树(No.100)
class Solution100:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
if not p and not q:
return True
if not p or not q:
return False
if p.val == q.val:
return self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)
else:
return False6.2.7 另一棵树的子树(No.572)
class Solution572:
def isSubtree(self, root: TreeNode, subRoot: TreeNode) -> bool:
# 遍历每个节点,判断是否是相同的树
if not root:
return False
return self.is_same_tree(root,subRoot) or self.isSubtree(root.left,subRoot) or self.isSubtree(root.right,subRoot)
def is_same_tree(self,a,b):
if not a and not b:
return True
if not a or not b:
return False
if a.val == b.val:
return self.is_same_tree(a.left,b.left) and self.is_same_tree(a.right,b.right)
else:
return False7. DFS/回溯算法
7.1 典型例题
7.1.1 字符串的排列(No.JZ38)
class SolutionJZ38(object):
def permutation(self, s):
"""
:type s: str
:rtype: List[str]
"""
c,res = list(s),[]
def recur(x):
if x == len(c) - 1:
res.append(''.join(c))
return
# 去重
d = set()
for i in range(x,len(c)):
if c[i] in d:
continue
d.add(c[i])
# 换固定点
c[i], c[x] = c[x], c[i]
recur(x+1)
# 回溯
c[i], c[x] = c[x], c[i]
recur(0)
return res
# res,path = [],[]
# char = list(s)
# def recur(n,used):
# if len(path)==n:
# res.append(''.join(path))
# return
# d = set()
# for i in range(n):
# if used[i] == 1: continue
# if char[i] in d: continue
# d.add(char[i])
# path.append(char[i])
# used[i] = 1
# recur(n,used)
# path.pop()
# used[i] = 0
# used = [0] * len(char)
# recur(len(char),used)
# return res7.1.2 子集(No.78)
class Solution78(object):
def subsets(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res,path = [[]],[]
def recur(n,idx):
if idx==n:
return
for i in range(idx,n):
path.append(nums[i])
res.append(list(path))
recur(n,i+1)
path.pop()
recur(len(nums),0)
return res7.1.3 组合(No.77)
class Solution77:
def combine(self, n: int, k: int) -> List[List[int]]:
# 回溯
def recur(idx):
if len(path) == k:
res.append(list(path))
return
# for i in range(idx,n):
for i in range(idx,n - (k-len(path)) + 1): # 剪枝
path.append(nums[i])
recur(i+1)
path.pop()
nums = [i+1 for i in range(n)]
res,path = [],[]
recur(0)
return res7.1.4 全排列(No.46)
class Solution46(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res,path = [],[]
def recur(n,used):
if len(path)==n:
res.append(list(path)) # 由于list是可变对象,此处不能直接append
return
for i in range(n):
if used[i]: continue
used[i] = 1
path.append(nums[i])
recur(n,used)
path.pop()
used[i] = 0
used = [0] * len(nums)
recur(len(nums),used)
return res7.1.5 全排列II(No.47)
class Solution47:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
def recur(used):
if len(path) == n:
res.append(list(path))
return
dic = set()
for i in range(n):
if used[i]: continue
if nums[i] in dic: continue # 去重
# if i>0 and nums[i] == nums[i-1] and not used[i-1]: continue 需对数组先排序
dic.add(nums[i])
path.append(nums[i])
used[i] = 1
recur(used)
used[i] = 0
path.pop()
res, path = [], []
n = len(nums)
used = [0] * n
recur(used)
return res7.1.6 单词搜索(No.79)
class Solution79:
def exist(self, board: List[List[str]], word: str) -> bool:
# 回溯
def dfs(i,j,idx):
if idx == n:
return True
if i < 0 or j < 0 or i == len(board) or j == len(board[0]):
return False
if board[i][j] != word[idx] or board[i][j] == 0:
return False
temp = board[i][j]
board[i][j] = 0
res = dfs(i-1,j,idx+1) or dfs(i+1,j,idx+1) or dfs(i,j-1,idx+1) or dfs(i,j+1,idx+1)
board[i][j] = temp
return res
n = len(word)
for i in range(len(board)):
for j in range(len(board[0])):
if board[i][j] == word[0]:
if dfs(i,j,0):
return True
return False7.1.7 排列序列(No.60)
class Solution60:
def getPermutation(self, n: int, k: int) -> str:
# DFS + 剪枝
def dfs(k,idx):
if idx == n:
return
cnt = jiecheng[n-1-idx]
for i in range(n):
if uesd[i]: continue
if cnt < k:
k -= cnt
continue
path.append(str(nums[i]))
uesd[i] = 1
dfs(k,idx + 1)
return # 直接返回即可,后续的不用遍历
nums = [i+1 for i in range(n)]
path = []
uesd = [0] * n
jiecheng = [1] * n
for i in range(1,n):
jiecheng[i] = i * jiecheng[i-1]
dfs(k,0)
return ''.join(path)
# 按位找规律,位上的值确定:num = nums[k // jc] if k % jc else nums[k // jc - 1]
# def jiecheng(n):
# res = 1
# while n > 1:
# res *= n
# n = n-1
# return res
# def recur(n,k):
# if n == 0:
# return
# jc = (jiecheng(n-1))
# num = nums[k // jc] if k % jc else nums[k // jc - 1]
# nums.remove(num)
# res.append(str(num))
# k = k % jc
# recur(n-1,k)
# nums = [i+1 for i in range(n)]
# res = []
# recur(n,k)
# return ''.join(res)7.1.8 矩阵中的路径(No.JZ12)
class SolutionJZ12:
def exist(self, board: List[List[str]], word: str) -> bool:
def dfs(i,j,idx):
if i<0 or j<0 or i>=m or j>=n or board[i][j] != word[idx]:
return False
if idx == len(word) - 1:
return True
temp = board[i][j]
board[i][j] = 0
res = dfs(i-1,j,idx+1) or dfs(i+1,j,idx+1) or dfs(i,j-1,idx+1) or dfs(i,j+1,idx+1)
board[i][j] = temp
return res
m, n = len(board), len(board[0])
for i in range(m):
for j in range(n):
if board[i][j] == word[0]:
if dfs(i,j,0): return True
return False7.1.9 岛屿数量(No.200)
class Solution200(object):
def numIslands(self, grid):
"""
:type grid: List[List[str]]
:rtype: int
"""
# DFS
def dfs(i,j):
if i < 0 or j < 0 or i == m or j == n or grid[i][j] == "0":
return
grid[i][j] = "0"
dfs(i-1,j)
dfs(i+1,j)
dfs(i,j-1)
dfs(i,j+1)
return
# BFS
def bfs(i,j):
quene = [[i,j]]
while quene:
i,j = quene.pop(0)
if i >= 0 and j >=0 and i < m and j < n and grid[i][j] == "1":
grid[i][j] = "0"
quene + [bfs(i-1,j),bfs(i+1,j),bfs(i,j-1),bfs(i,j+1)]
m,n = len(grid), len(grid[0])
res = 0
for i in range(m):
for j in range(n):
if grid[i][j] == "1":
dfs(i,j)
res += 1
return res<Paste>7.1.10 岛屿的最大面积(No.695)
class Solution695:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
# DFS
def dfs(i,j):
if i < 0 or j < 0 or i == m or j == n or grid[i][j] == 0:
return 0
grid[i][j] = 0
return 1 + dfs(i-1,j) + dfs(i+1,j) + dfs(i,j-1) + dfs(i,j+1)
m,n = len(grid),len(grid[0])
res = 0
for i in range(m):
for j in range(n):
if grid[i][j] == 1:
res = max(res, dfs(i,j))
return res7.1.11 不同岛屿的数量(No.694)
class Solution694:
def numDistinctIslands(self, grid: List[List[int]]) -> int:
# DFS+路径去重
def dfs(i,j,o_i,o_j):
if i < 0 or j < 0 or i == m or j == n or grid[i][j] == 0:
return
grid[i][j] = 0
# 记录相对路径
temp.append(str(i-o_i))
temp.append(str(j-o_j))
dfs(i-1,j,o_i,o_j)
dfs(i+1,j,o_i,o_j)
dfs(i,j-1,o_i,o_j)
dfs(i,j+1,o_i,o_j)
return
m,n = len(grid),len(grid[0])
res = set()
for i in range(m):
for j in range(n):
if grid[i][j] == 1:
temp = []
dfs(i,j,i,j)
res.add(''.join(temp))
return len(res)7.1.12 岛屿的周长(No.463)
class Solution463:
def islandPerimeter(self, grid: List[List[int]]) -> int:
# DFS 碰到水或者越界次数等于周长
def dfs(i,j):
if i < 0 or j < 0 or i == m or j == n or grid[i][j] == 0:
return 1
if grid[i][j] == 2: # 走过的路,不能标记为0了
return 0
grid[i][j] = 2
return dfs(i-1,j) + dfs(i+1,j) + dfs(i,j-1) + dfs(i,j+1)
m,n = len(grid),len(grid[0])
for i in range(m):
for j in range(n):
if grid[i][j] == 1:
return dfs(i,j)7.1.13 最大人工岛(No.827)
class Solution827:
def largestIsland(self, grid: List[List[int]]) -> int:
# DFS
def dfs(i,j,idx):
if i < 0 or j < 0 or i == n or j == n or grid[i][j] != 1:
return 0
grid[i][j] = idx # 岛屿序号,2,3,4,...
return 1 + dfs(i-1,j,idx) + dfs(i+1,j,idx) + dfs(i,j-1,idx) + dfs(i,j+1,idx)
def final_area(i,j):
area,idxs = 0,set()
dirs = [(-1,0),(1,0),(0,-1),(0,1)] # 四个方向
for d in dirs:
n_i,n_j = i + d[0], j + d[1]
if n_i < 0 or n_j < 0 or n_i == n or n_j == n or grid[n_i][n_j] == 0:
continue
idx = grid[n_i][n_j]
if idx not in idxs: # 只考虑idx不同的
idxs.add(idx)
area += dic[idx]
else:
continue
return 1 + area
n,idx,dic,res = len(grid),2,dict(),0
# 遍历陆地,计算岛屿面积并标记序号
for i in range(n):
for j in range(n):
if grid[i][j] == 1:
area = dfs(i,j,idx)
dic[idx] = area # 序号:面积
idx += 1
res = max(res, area)
if res == 0: return 1 # 无陆地,造1
# 遍历海洋,计算周围岛屿总面积
for i in range(n):
for j in range(n):
if grid[i][j] == 0:
res = max(res, final_area(i,j))
return res7.1.14 组合总和(No.39)
class Solution39:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
# 动态规划,完全背包求具体方案, dp[j]表示和为j的组合方案
# m,n = len(candidates), target+1
# dp = {i:[] for i in range(n)}
# for i in range(m):
# for j in range(n):
# if j > candidates[i]:
# dp[j].extend([x+[candidates[i]] for x in dp[j-candidates[i]]])
# elif j == candidates[i]:
# dp[j].extend([[candidates[i]]])
# return dp[target]
# 回溯+剪枝
def dfs(idx,target):
if target==0:
res.append(list(path))
return
if target < 0: return
for i in range(idx,n):
# 剪枝
if target < candidates[i]:
break
target -= candidates[i]
path.append(candidates[i])
dfs(i,target) # 每一个元素可以重复利用,因此从i开始
target += candidates[i]
path.pop()
res,path = [],[]
candidates = sorted(candidates) # 排序是剪枝的前提
n = len(candidates)
dfs(0,target)
return res7.1.15 子集II(No.90)
class Solution90:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
# 回溯
def dfs(idx):
if idx == n:
return
for i in range(idx,n):
if i > idx and nums[i] == nums[i-1]: continue # 同一树层去重
path.append(nums[i])
res.append(list(path))
dfs(i+1)
path.pop()
res,path = [[]],[]
nums = sorted(nums) # 去重前需排序
n = len(nums)
dfs(0)
return res7.2 典型例题
7.2.1 组合总和II(No.40)
class Solution40:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
# 回溯
def dfs(idx, target):
if target == 0:
res.append(list(path))
return
if target < 0: return
for i in range(idx, n):
if i > idx and candidates[i] == candidates[i-1]: # 树层去重
continue
if target < candidates[i]: # 剪枝
break
target -= candidates[i]
path.append(candidates[i])
dfs(i+1, target)
target += candidates[i]
path.pop()
n = len(candidates)
candidates = sorted(candidates)
res,path = [],[]
dfs(0,target)
return res7.2.2 组合总和III(No.216)
class Solution216:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
# 回溯
def dfs(idx, target):
if len(path) == k and target == 0:
res.append(list(path))
return
if target < 0 or len(path) > k:
return
for i in range(idx,9):
if target < nums[i]: # 剪枝
break
target -= nums[i]
path.append(nums[i])
dfs(i+1,target)
target += nums[i]
path.pop()
nums = [i+1 for i in range(9)]
res, path = [],[]
dfs(0,n)
return res7.2.3 电话号码的字母组合(No.17)
class Solution17:
def letterCombinations(self, digits: str) -> List[str]:
# 回溯
def dfs(idx):
if idx == n:
res.append(''.join(path))
return
num = digits[idx]
# 遍历每个数字对应的字母
for char in dic[num]:
path.append(char)
dfs(idx+1)
path.pop()
if not digits: return []
dic = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'}
res,path,n = [],[],len(digits)
dfs(0)
return res
# 队列
# if not digits: return []
# quene = ['']
# dic = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'}
# for num in digits:
# chars = dic[num]
# size = len(quene)
# for i in range(size):
# temp = quene.pop(0)
# for char in chars:
# quene.append(temp+char)
# return quene7.2.4 分割回文串(No.131)
class Solution131:
def partition(self, s: str) -> List[List[str]]:
# 回溯
def is_huiwen(s):
return s == s[::-1]
def dfs(idx):
if idx == n:
res.append(list(path))
return
for i in range(idx, n):
head = s[idx:i+1]
# if not is_huiwen(head): # 如果前缀不是回文,直接跳过
if not dp[idx][i]:
continue
path.append(head)
dfs(i+1)
path.pop()
# 优化,动态规划求每个子串是否为回文串,dp[i][j]表示s[i:j+1]是否为回文串
res,path,n = [],[],len(s)
dp = [[False]*n for _ in range(n)]
for i in range(n):
dp[i][i] = True
for i in range(n-1,-1,-1):
for j in range(i+1,n):
dp[i][j] = s[i] == s[j] and (dp[i+1][j-1] or j-i==1)
dfs(0)
return res7.2.5 复原IP地址(No.93)
class Solution93:
def restoreIpAddresses(self, s: str) -> List[str]:
# 回溯
def dfs(idx):
if (n-idx) > (4-len(path))*3 or (n-idx) < (4-len(path)): # 剪枝
return
if idx == n:
if len(path)==4:
res.append('.'.join(path))
return
if idx+3>n:
right = n
else:
right = idx + 3
for i in range(idx,right):
num = s[idx:i+1]
if int(num) > 255 or (len(num) > 1 and num[0] == '0'):
continue
path.append(num)
dfs(i+1)
path.pop()
res,path,n = [],[],len(s)
dfs(0)
return res7.2.6 二叉树中的最大路径和(No.124)
class Solution124:
def maxPathSum(self, root: TreeNode) -> int:
def dfs(root):
if not root:
return 0
left = dfs(root.left)
right = dfs(root.right)
# 当前子树的最大路径和
cur_sum = root.val + left + right
self.res = max(self.res, cur_sum)
# 作为子树对外的最大路径和
out_sum = max(left+root.val, right+root.val)
return out_sum if out_sum > 0 else 0
self.res = -float('inf') # 考虑负数情况,不能设为0
dfs(root)
return self.res7.2.7 N皇后(No.51)
class Solution51:
def solveNQueens(self, n: int) -> List[List[str]]:
# 回溯,每行只能放一个皇后
def dfs(row):
if row == n:
res.append([''.join(i) for i in grid])
return
# 遍历列
for i in range(n):
if is_valid(row,i):
grid[row][i] = 'Q'
dfs(row+1)
grid[row][i] = '.'
return
def is_valid(row,col):
for i in range(row):
if grid[row-i-1][col] == 'Q': # 上方
return False
if col-i-1>=0 and grid[row-i-1][col-i-1] == 'Q': # 左上方
return False
if col+i+1<n and grid[row-i-1][col+i+1] == 'Q': # 右上方
return False
return True
res = []
grid = [['.']*n for _ in range(n)]
dfs(0)
return res7.2.8 括号生成(No.22)
class Solution22:
def generateParenthesis(self, n: int) -> List[str]:
# 回溯,left,right分别为左右括号剩余个数
def dfs(left,right):
if left==0 and right==0:
res.append(''.join(path))
return
# 不满足有效括号
if left>right:
return
if left > 0:
path.append('(')
left -= 1
dfs(left,right)
left += 1
path.pop()
if right > 0:
path.append(')')
right -= 1
dfs(left,right)
right += 1
path.pop()
res,path = [],[]
dfs(n,n)
return res8. 栈、队列、堆
8.1 典型例题
8.1.1 用两个栈实现队列(No.JZ9)
class CQueue(jobject):
def __init__(self):
self.s1 = []
self.s2 = []
def appendTail(self, value):
"""
:type value: int
:rtype: None
"""
self.s1.append(value)
def deleteHead(self):
"""
:rtype: int
"""
# 将s1中的元素依次出栈到s2中
if self.s2:
return self.s2.pop()
else:
if self.s1:
for i in range(len(self.s1)):
self.s2.append(self.s1.pop())
return self.s2.pop()
else:
return -18.1.2 滑动窗口的最大值(No.JZ59I)
class SolutionJZ59I(object):
def maxSlidingWindow(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
if not nums:
return []
# 动态规划
# dp = [0] * (len(nums)-k+1)
# dp[0] = max(nums[:k])
# for i in range(1, len(dp)):
# if nums[i-1] != dp[i-1]:
# dp[i] = max(dp[i-1], nums[i + k - 1])
# else:
# dp[i] = max(nums[i:i+k])
# return dp
# 单调队列
res, quene = [], []
for i,j in zip(range(1-k,len(nums)-k+1), range(len(nums))):
if i > 0 and quene[0] == nums[i-1]:
quene.pop(0)
while quene and quene[-1] < nums[j]:
quene.pop()
quene.append(nums[j])
if i >= 0:
res.append(quene[0])
return res8.1.3 包含min函数的栈(No.JZ30)
class MinStack:
def __init__(self):
"""
initialize your data structure here.
"""
self.stack = []
# 辅助栈,单调减
self.m = []
def push(self, x: int) -> None:
self.stack.append(x)
if not self.m or x <= self.m[-1]:
self.m.append(x)
def pop(self) -> None:
num = self.stack.pop()
if num == self.m[-1]:
self.m.pop()
def top(self) -> int:
return self.stack[-1]
def min(self) -> int:
return self.m[-1]8.1.4 队列的最大值(No.JZ59II)
class MaxQueue:
def __init__(self):
self.a = []
self.b = []
def max_value(self) -> int:
if not self.b:
return -1
else:
return self.b[0]
def push_back(self, value: int) -> None:
self.a.append(value)
# 维护一个双端队列,删除队列中所有小于新入队的元素,保持单调减
while self.b and self.b[-1] < value:
self.b.pop()
self.b.append(value)
def pop_front(self) -> int:
if not self.a:
return -1
num = self.a.pop(0)
if num == self.b[0]:
self.b.pop(0)
return num8.1.5 数据流中的中位数(No.JZ41)
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
# self.quene = []
self.a = [] # 小顶堆,存较大的一半数
self.b = [] # 大顶堆,存较小的一半数
def addNum(self, num: int) -> None:
# 队列,保持数组有序
# if not self.quene:
# self.quene.append(num)
# return
# l,r = 0,len(self.quene)-1
# while l<=r:
# mid = (l+r)//2
# if self.quene[mid] > num:
# r = mid - 1
# else:
# l = mid + 1
# self.quene.insert(l,num)
# 堆
if len(self.a) == len(self.b):
heapq.heappush(self.b, -num)
heapq.heappush(self.a, -heapq.heappop(self.b))
else:
heapq.heappush(self.a, num)
heapq.heappush(self.b, -heapq.heappop(self.a))
def findMedian(self) -> float:
# m = (len(self.quene)-1) // 2
# if len(self.quene) % 2 == 1:
# return self.quene
# else:
# return (self.quene[m] + self.quene[m+1])/2
if len(self.a) == len(self.b):
return (self.a[0] - self.b[0]) / 2
else:
return self.a[0]8.1.6 栈的压入、弹出序列(No.JZ31)
class SolutionJZ31:
def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
# 辅助栈,模拟过程
stack,i = [],0
for num in pushed:
stack.append(num)
while stack and stack[-1]==popped[i]:
stack.pop()
i += 1
return not stack8.1.7 有效的括号(No.20)
class Solution20:
def isValid(self, s: str) -> bool:
# 辅助栈
stack = []
for i in range(0,len(s)):
if not stack:
stack.append(s[i])
elif stack[-1]=='(' and s[i]==')' or stack[-1]=='{' and s[i]=='}' or stack[-1]=='[' and s[i]==']':
stack.pop()
else:
stack.append(s[i])
return False if stack else True8.1.8 字符串解码(No.394)
class Solution394:
def decodeString(self, s: str) -> str:
# 辅助栈,涉及括号匹配问题适合用栈来解决
stack,res,num = [],'',0
for char in s:
if '0' <= char <= '9':
num = num*10 + int(char) # 转数字,考虑多位数字情况
elif char == '[':
stack.append((res,num))
res,num = '',0
elif char == ']':
last_res, last_num = stack.pop()
res = last_res + last_num * res
else:
res += char
return res8.1.9 每日温度(No.739)
class Solution739:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
# 单调栈,栈中记录元素下标即可
n = len(temperatures)
res = [0] * n
stack = [0]
for i in range(1,n):
while stack and temperatures[i] > temperatures[stack[-1]]:
idx = stack.pop()
res[idx] = i - idx
stack.append(i)
return res8.1.10 基本计算器(No.224,No.227,No.772)
class Solution224:
def calculate(self, s: str) -> int:
# 双栈处理,通用模板
def calc(num_stack,op_stack):
y,x = num_stack.pop(),num_stack.pop()
op = op_stack.pop()
if op == '+':
ans = x + y
elif op == '-':
ans = x - y
elif op == '*':
ans = x * y
elif op == '/':
ans = x // y
num_stack.append(ans)
priority = {'+':1,'-':1,'*':2,'/':2}
# 预处理字符串,处理空格,首位补零
s = '(' + s.replace(' ','').replace('(-','(0-') +')'
n = len(s)
num_stack,op_stack = [0],[] # 分别存数字和运算符,防止为负数num需添0
i= 0
while i < n:
c = s[i]
i += 1
if c.isdigit(): # 数字
num = int(c)
while i < n and s[i].isdigit():
num = num * 10 + int(s[i])
i += 1
num_stack.append(num)
elif c == '(':
op_stack.append(c)
elif c== ')':
# 计算直至遇到'('
while op_stack and op_stack[-1] != '(':
calc(num_stack, op_stack)
op_stack.pop()
else:
while op_stack and op_stack[-1] != '(':
prev_op = op_stack[-1]
# 只有「栈内运算符」比「当前运算符」优先级高/同等,才进行运算
if priority[prev_op] < priority[c]:
break
calc(num_stack, op_stack)
op_stack.append(c)
return num_stack[-1]8.1.11 柱状图中最大的矩形(No.84)
class Solution84:
def largestRectangleArea(self, heights: List[int]) -> int:
n = len(heights)
res = 0
# 先放入哨兵结点,在循环中就不用做非空判断
heights = [0] + heights + [0]
stack = [0]
n += 2
for i in range(1, n):
while heights[i] < heights[stack[-1]]:
cur_height = heights[stack.pop()]
cur_width = i - stack[-1] - 1
res = max(res, cur_height * cur_width)
stack.append(i)
return res9. 排序
9.1 典型例题
9.1.1 数组中的逆序对(No.JZ51)
class SolutionJZ51(object):
def reversePairs(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# 暴力解法超时
# res = 0
# for i in range(len(nums)):
# for j in range(i+1,len(nums)):
# if nums[i] > nums[j]:
# res += 1
# return res
# 归并排序
def merge_sort(l,r):
if l >= r:
return 0
mid = (l + r) // 2
res = merge_sort(l, mid) + merge_sort(mid+1, r)
# merge
i, j = l, mid + 1
temp[l:r+1] = nums[l:r+1]
for k in range(l, r+1):
if i == mid+1:
nums[k] = temp[j]
j += 1
elif j == r + 1 or temp[i] <= temp[j]:
nums[k] = temp[i]
i += 1
elif temp[i] > temp[j]:
nums[k] = temp[j]
j += 1
res += mid - i + 1
return res
temp = [0] * len(nums)
res = merge_sort(0,len(nums)-1)
return res9.1.2 最小的k个数(No.JZ40)
class SolutionJZ40(object):
def getLeastNumbers(self, arr, k):
"""
:type arr: List[int]
:type k: int
:rtype: List[int]
"""
# return sorted(arr)[:k]
# 快排
# def sort(l,r):
# if l >= r:
# return
# i,j = l,r
# while i < j:
# while i < j and arr[j]>=arr[l]: j -= 1
# while i < j and arr[i]<=arr[l]: i += 1
# arr[i], arr[j] = arr[j], arr[i]
# arr[l],arr[i] = arr[i], arr[l]
# sort(l,i-1)
# sort(i+1,r)
# sort(0,len(arr)-1)
# return arr[:k]
# 快排优化
def sort(l,r):
if l >= r:
return
i,j = l,r
while i < j:
while i < j and arr[j]>=arr[l]: j -= 1
while i < j and arr[i]<=arr[l]: i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[l],arr[i] = arr[i], arr[l]
if i + 1 == k:
return
elif i + 1 > k:
sort(l,i-1)
else:
sort(i+1,r)
sort(0,len(arr)-1)
return arr[:k]9.1.3 把数组排成最小的数(No.JZ45)
class SolutionJZ45(object):
def minNumber(self, nums):
"""
:type nums: List[int]
:rtype: str
"""
# 自定义排序规则+快速排序
def quick_sort(l,r):
if l >= r: return
i,j = l,r
while i < j:
while i < j and int(nums[j]+nums[l]) >= int(nums[l]+nums[j]): j -= 1
while i < j and int(nums[i]+nums[l]) <= int(nums[l]+nums[i]): i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[l],nums[i] = nums[i], nums[l]
quick_sort(l,i-1)
quick_sort(i+1,r)
nums = [str(i) for i in nums]
quick_sort(0,len(nums)-1)
return ''.join(nums)9.1.4 数组中的第K个最大元素(No.215)
class Solution215:
def findKthLargest(self, nums: List[int], k: int) -> int:
def quick_sort(l,r):
if l >= r:
return
i,j = l,r
base = (l+r)//2
nums[base],nums[l] = nums[l],nums[base]
while i < j:
while i < j and nums[j] <= nums[l]: j -= 1
while i < j and nums[i] >= nums[l]: i += 1
nums[i],nums[j] = nums[j],nums[i]
nums[l],nums[i] = nums[i],nums[l]
if i == k-1:
return
elif i > k-1:
quick_sort(l,i-1)
else:
quick_sort(i+1,r)
# 快排
# n = len(nums) - 1
# quick_sort(0,n)
# return nums[k-1]
# 堆排
heap = []
for i in nums:
heapq.heappush(heap,i)
if len(heap) > k:
heapq.heappop(heap)
return heap[0]10. 位运算
10.1 典型例题
10.1.1 数组中数字出现的次数(No.JZ56I)
class SolutionJZ56I:
def singleNumbers(self, nums: List[int]) -> List[int]:
# 异或^可以剔除出现2次的数字
ans = 0
for i in nums:
ans ^= i
# ans = a ^ b,a、b即为只出现一次的数字
m = 1
while m & ans == 0:
m <<= 1
a,b = 0,0
for i in nums:
if i & m: a ^= i
else: b ^= i
return a,b10.1.2 二进制中1的个数(No.JZ15)
n-1可将n最右边的1变为0,此1右边的0都变为1n&(n-1)可将n最右边的1变成0,其余不变class SolutionJZ15: def hammingWeight(self, n: int) -> int: # 位运算 res,point = 0,1 for i in range(32): if n & point: res += 1 point <<= 1 return res # 利用n&(n-1) # res = 0 # while n: # n &= n-1 # res += 1 # return res
10.1.3 数组中数字出现的次数II(No.JZ56II)
class SolutionJZ56II:
def singleNumber(self, nums: List[int]) -> int:
# 哈希表
# dic = {}
# for num in nums:
# if num not in dic:
# dic[num] = 0
# dic[num] += 1
# for i in dic:
# if dic[i] == 1:
# return i
# 位运算,统计各位上1的个数,再对3取余,剩下的就是结果
arr = [0] * 32
for i in range(len(nums)):
for j in range(32):
arr[j] += nums[i]&1
nums[i] >>= 1
res,k = 0,3
for i in range(32):
res <<= 1
res |= arr[31-i] % 3
return res10.1.4 不用加减乘除做加法(No.JZ65)
class SolutionJZ65:
def add(self, a: int, b: int) -> int:
# Python,Java 等语言中的数字都是以补码形式存储的。但Python没有int,long等不同长度变量,即在编程时无变量位数的概念
x = 0xffffffff
a,b = a & x,b & x # 可理解为舍去此数字32位以上的数字(将32位以上都变为0),从无限长度变为一个32位整数
while b!=0:
a,b = a ^ b, (a & b) << 1 & x # a存储无进位和,b存储进位
return a if a <= 0x7fffffff else ~(a ^ x) # 还原python存储格式,若为负数,需要将大于32的所有位置1x. 其他
x.1 其他例题
x.1.1 x的平方根(No.69)
class Solution69(object):
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
# 二分法
# if x <= 1:
# return x
# left = 1
# right = x // 2 + 1
# while right - left > 1:
# mid = (left+right)//2
# if mid**2 == x:
# return mid
# elif mid**2 < x:
# left = mid
# else:
# right = mid
# return left
# 牛顿迭代法
if x <= 1:
return x
x0, C = float(x), float(x)
while True:
xi = C/(2*x0) + x0/2
if x0 - xi < 1e-6:
break
x0 = xi
return int(xi)x.1.2 1~n 整数中 1 出现的次数(No.JZ43)
class SolutionJZ43(object):
def countDigitOne(self, n):
"""
:type n: int
:rtype: int
"""
# 直接暴力内存炸了,需要从位数的角度分析
high = n // 10
cur = n % 10
low = 0
digit = 1
res = 0
for i in range(len(str(n))):
if cur==0:
res += high*digit
elif cur==1:
res += high*digit + low +1
else:
res += (high+1)*digit
low += cur*digit
cur = high % 10
high //= 10
digit *= 10
return resx.1.3 Pow(x, n)(No.50)
class Solution50:
def myPow(self, x: float, n: int) -> float:
# 递归
def recur(n):
if n == 0:
return 1.0
ans = recur(n // 2)
if n % 2:
return ans * ans * x
else:
return ans * ans
return recur(n) if n>=0 else 1.0/recur(-n)x.1.4 数字序列中某一位的数字(No.JZ44)
class SolutionJZ44:
def findNthDigit(self, n: int) -> int:
# 找规律,先确定数位,再确定哪个数,最后确定在数的第几位
digit, start, count = 1,1,9
while n > count:
n -= count
digit += 1
start *= 10
count = 9 * start * digit
num = start + (n-1)//digit
k = (n-1) % digit
return int(str(num)[k])x.1.5 用Rand7()实现Rand10()(No.470)
class Solution470:
def rand10(self):
"""
:rtype: int
"""
# 关键:(randx() - 1) * y + randy() 能够构造randx*y()
num = (rand7() - 1) * 7 + rand7() # 构造rand49()
# while num > 10:
# num = (rand7() - 1) * 7 + rand7()
# return num
while num > 40:
num = (rand7() - 1) * 7 + rand7()
return 1 + num % 10x.1.6 整数反转(No.7)
class Solution7:
def reverse(self, x: int) -> int:
sign = 1
if x < 0:
sign = 0
x = -x
res = 0
while x > 0:
digit = x % 10
# 判断是否溢出
if res > (2**31-1)//10 or res == (2**31-1)//10 and digit==7:
return 0
x = x // 10
res = res * 10 + digit
return res if sign else -res